Ejercicios con raíces cuadradas

1
Ejercicios para raíces cuadradas
1. Un cuadrado y un círculo tienen la misma área.
  El radio del círculo es de 13,6 cm. ¿Cuál es la longitud del lado del cuadrado?
  
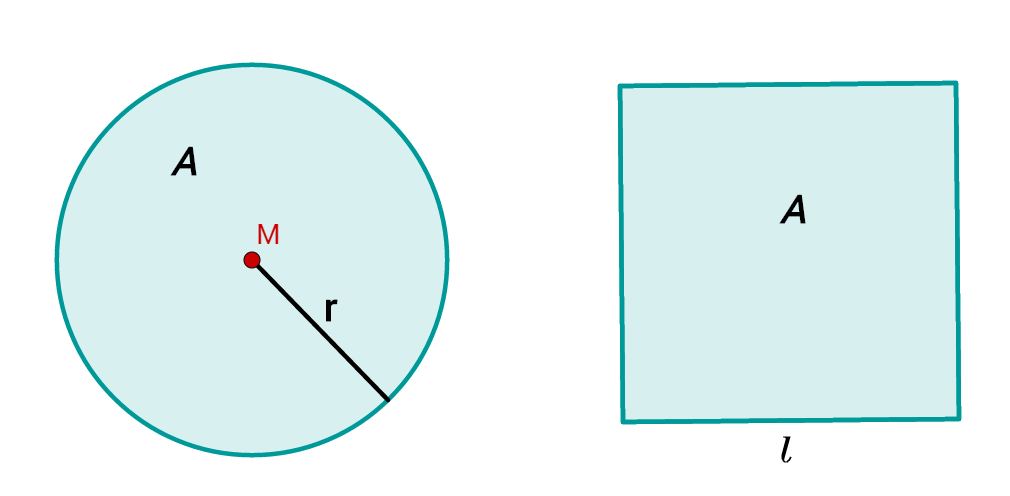
  El lado del cuadrado
  Ya sabes:
  $A_{círculo}=A_{cuadrado}=581{,}07 cm^2$
  Ten a la mano la fórmula para calcular el área del cuadrado.
  $\displaystyle A_{cuadrado}=l^2$
  $A_{cuadrado}=l^2$
  aplica la raíz cuadrada utilizando el radical.
  $\sqrt{A_{cuadrado}}=\pm l$
  Al resolver la raíz cuadrada obtienes dos soluciones.
  $\sqrt{581.07 cm^2}=\pm l$
  Las dos soluciones que obtienes son:
  $l_{solución 1}=-24{,}11cm$
  $l_{solución 2}=24{,}11cm$
  Atención: En el contexto del cuadrado, sólo una de las soluciones parece tener sentido.
  Como la longitud del lado del cuadrado no puede ser negativa, la solución correcta es: $l = 24.11 c m$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  Primero tienes que calcular el área del círculo, para saber qué tan grande tiene que ser el área del cuadrado.
  Se da el radio $r = 13,6 c m$
  Calcula el área usando la fórmula.
  $\displaystyle A_{círculo}=\pi r^2$
  $A_{círculo}=\pi r^2$
  Esta es el área que tambien tiene el cuadrado
  $A_{círculo}=\pi \cdot (13{,}6)^2$
  $A_{círculo} \approx 581{,}07cm^2$
2. ¿Qué raíz o raíces cumplen con la definición?
  $\sqrt{25}$
  $\sqrt{7-3}$
  $\sqrt{-25}$
  $\sqrt{5-7}$
3. ¿Qué raíz o raíces cumplen con la definición?
  $5^\dfrac{1}{2}$
  $\sqrt{2}$
  $\sqrt{-3}$
  $(-5)^\dfrac{1}{2}$
2
Ejercicios de cálculo con raíces cuadradas
1. Simplifica y calcula:
  $7\sqrt{9}+5\sqrt{3^2+4^2}+5\sqrt{3}−3\sqrt{3}$
  
  La solución es: $46+2\sqrt{3}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $7\sqrt{9}+5\sqrt{3^2+4^2}+5\sqrt{3}−3\sqrt{3}$ =
  Toma la raiz $\sqrt{9}$ y calcula.
  $=7\cdot3+5\sqrt{3^2+4^2}+5\sqrt{3}−3\sqrt{3}=$
  $=$ $21+5\sqrt{3^2+4^2}+5\sqrt{3}−3\sqrt{3}=$
  Calcula los números al cuadrado y simplifica.
  $=21+5\sqrt{9+16}+5\sqrt{3}−3\sqrt{3}=$
  $=21+5\sqrt{25}+5\sqrt{3}−3\sqrt{3}=$
  Toma la raiz $\sqrt{25}$ y calcula.
  $=21+5\cdot5+5\sqrt{3}−3\sqrt{3}=$
  $=21+25+5\sqrt{3}−3\sqrt{3}=$
  $=46+5\sqrt{3}−3\sqrt{3}=$
  Simplifica las raíces usando la ley de la raíz cuadrada de la substracción.
  $=46+(5−3)3\sqrt{3}= 46+2\sqrt{3}$
3
Resuelve las siguientes igualdades
1. $x^{2} = 16$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raiz Cuadrada
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $x^{2} = 16$
  Utiliza el radical
  $\sqrt{x^2}=\sqrt{16}$
  $\vert x \vert=4$
  Las soluciones son:
  $x_\text{Solucion 1}=4\\x_\text{Solucion 2}=-4$
2. $x^{2} = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raiz Cuadrada
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $x^{2} = 0$
  Utiliza el radica
  $\sqrt{x^2}=\sqrt{0}$
  $∣ x ∣ = 0$
  La solución es $x = 0$
3. $x^{2}+2=11$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raiz Cuadrada
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $x^{2}+2=11$
  Cambia el $2$ de lado en la igualdad
  $x^{2}=11-2\\x^{2}=9\\$
  Utiliza el radical
  $\sqrt{x^2}=\sqrt{9}\\\vert x \vert=3$
  Las soluciones son:
  $x_\text{Solucion 1}=3\\x_\text{Solucion 2}=-3$
4. $4 + x^{2} = 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raiz cuadrada
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $4 + x^{2} = 2$
  Cambia el $4$ de lado en la igualdad
  $x^2=2-4\\x^2=-2$
  Utiliza el radical
  $\sqrt{x^2}=\sqrt{-2}$
  Aquí no hay solución. No se puede sacar una raíz de un número negativo.
4
Simplifica si es posible:
1. $5\sqrt{3}+2\sqrt{3}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la adición de raíces
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $5\sqrt{3}+2\sqrt{3}=$
  Utiliza la ley para la adición de raíces
  $(5+2)\sqrt{3}=$
  Resuelve la suma
  $=7\sqrt{3}$
2. $6\sqrt{4}-2\sqrt{4}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la sustraer raíces
  Solución alternativa:
  
  También se puede calcular la solución sin las leyes raíz:
  $6\sqrt{4}-2\sqrt{4}=$
  resuelve las raíces
  $6\cdot2-2\cdot2=$
  calcula
  $12 - 4 = 8$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $6\sqrt{4}-2\sqrt{4}=$
  Utiliza la ley para restar raíces
  $(6-2)\sqrt{4}=$
  resuelve la resta
  $4\sqrt{4}=$
  resuelve la raíz
  $4\cdot2=8$
3. $3\sqrt{4}+3\sqrt{3}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la adición de raíces
  Podrías utilizar parentesis para el $3$ .
  $3(\sqrt{4}+\sqrt{3})$
  Sin embargo, solo llegas hasta aquí y esto no es muy útil.
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $3\sqrt{4}+3\sqrt{3}$
  Aquí no se puede utilizar la ley para la adición de raíces porque los radicandos no son iguales. Así que no se pueden sumar las raíces.
4. $\sqrt{3}\cdot\sqrt{7}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la multiplicación de raíces
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{3}\cdot\sqrt{7}=$
  Utiliza la ley para la multiplicación de raíces
  $\sqrt{3\cdot7}=$
  resuleve la multiplicación
  $=\sqrt{21}$
5. $\sqrt{2}\cdot\sqrt{8}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la multiplicación de raíces
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{2}\cdot\sqrt{8}=$
  Utiliza la ley para la multiplicación de raíces
  $\sqrt{2\cdot8}=$
  resuleve la multiplicación
  $\sqrt{16}=$
  resuelve la raíz
  $\sqrt{16}=4$
6. $\dfrac{\sqrt{27}}{\sqrt{3}}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley para la división de raíces
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\frac{\sqrt{27}}{\sqrt{3}}=$
  Utiliza la ley para la división de raíces
  $\sqrt\frac{27}{3}=\sqrt{9}=3$
7. $\sqrt{(-27)^2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley de la raíz como pontencia
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{(-27)^2}=$
  Utiliza la Ley de la raíz como pontencia
  $=\vert-27\vert=27$
8. $(\sqrt{2\cdot9})^2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley de la raíz como pontencia
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $(\sqrt{2\cdot9})^2=$
  Utiliza la Ley de la raíz como pontencia
  $(\sqrt{2\cdot9})^2=(\sqrt{18})^2=18$
9. $\sqrt{7}\cdot\sqrt{7}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: ley para la multiplicación de raíces
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{7}\cdot\sqrt{7}=$
  Utiliza la ley para la multiplicación de raíces
  $\sqrt{7}\cdot\sqrt{7}=7$
10. $25^\dfrac{1}{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ley de la raíz como pontencia
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $25^\dfrac{1}{2}=$
  Utiliza la Ley de la raíz como pontencia
  $=\sqrt{25}=5$
5
Ejercicios para hacer racionales los denominadores
Haz que el denominador sea racional. Simplificar al máximo:
1. $\frac{1}{\sqrt{2}}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hacer que el denominador sea racional
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\frac{1}{\sqrt{2}}=$
  Amplia la fraccion
  $=\frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}$
  $=\frac{\sqrt{2}}{(\sqrt{2})^2}$
  Resolver la raíz y la potencia
  $=\frac{\sqrt{2}}{2}$
2. $\dfrac{5}{2\sqrt{3}}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hacer que el denominador sea racional
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\dfrac{5}{2\sqrt{3}}=$
  Amplia la fraccion con $\sqrt{3}$
  $=\dfrac{5\cdot\sqrt{3}}{2\sqrt{3}\cdot\sqrt{3}}=\dfrac{5\sqrt{3}}{2\cdot3}=\dfrac{5}{2\cdot3}\sqrt{3}$
  simpifica
  $=\dfrac{5}{6}\sqrt{3}$
3. $\dfrac{25}{\sqrt{125}}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hacer que el denominador sea racional
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\dfrac{25}{\sqrt{125}}=$
  Resuleve parcialmente la raíz
  $=\dfrac{25}{\sqrt{25\cdot5}}$
  $=\dfrac{25}{5\sqrt{5}}$
  Amplia la fraccion con $\sqrt{5}$
  $=\dfrac{25\cdot\sqrt{5}}{5\sqrt{5}\cdot\sqrt{5}}=\dfrac{25\cdot\sqrt{5}}{5\cdot5}=\dfrac{25\cdot\sqrt{5}}{25}=$
  Simplifica
  $=\sqrt{5}$
4. $\dfrac{\sqrt{y}-\sqrt{y}}{\sqrt{xy}}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hacer que el denominador sea racional
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\dfrac{\sqrt{y}-\sqrt{y}}{\sqrt{xy}}=$
  Ampliar con el denominador
  $=\dfrac{(\sqrt{y}-\sqrt{y})\cdot\sqrt{xy}}{\sqrt{xy}\cdot\sqrt{xy}}=$
  $=\dfrac{\sqrt{x}\cdot\sqrt{xy}-\sqrt{y}\cdot\sqrt{xy}}{\sqrt{xy}^2}=$
  Resolver la raíz y la potencia
  $=\dfrac{\sqrt{x}^2\cdot\sqrt{y}-\sqrt{y}^2\cdot\sqrt{x}}{xy}=\dfrac{x\sqrt{y}-y\sqrt{x}}{xy}=$
  Separa la fracción
  $=\dfrac{x\sqrt{y}}{xy}-\dfrac{y\sqrt{x}}{xy}=$
  simplifica
  $=\dfrac{\sqrt{y}}{y}-\dfrac{\sqrt{x}}{x}=$
6
Tareas para términos con raíces cuadradas
1. Justifica que para el positivo $a$ se cumpla:
  $\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenciación
  Intenta que el denominador sea racional para esto.
  $\frac{1}{\sqrt{a}}$
  amplia la fracción con $\sqrt{a}$
  $=\frac{1\cdot\sqrt{a}}{\sqrt{a}\cdot\sqrt{a}}$
  Utiliza las leyes de cálculo del producto de raíces.
  $=\frac{1\cdot\sqrt{a}}{\sqrt{a\cdot a}}$
  El cuadrado y la raíz se anulan mutuamente.
  $=\frac{\sqrt{a}}{a}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  Quieres demostrar que $\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a}$
7
Saca la raíz lo más que puedas:
1. $\sqrt{20}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \sqrt{2\cdot2\cdot5}=$
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \sqrt{2^2\cdot5}=$
  Descompone la raíz:
  $\displaystyle \sqrt{2^2}\cdot\sqrt{5}=$
  Saca la raíz:
  $\displaystyle 2\cdot\sqrt{5}= 2\sqrt{5}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{20}=$
2. $\sqrt{27}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \sqrt{3\cdot3\cdot3}=$
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \sqrt{3^2\cdot3}=$
  Descompone la raíz:
  $\displaystyle \sqrt{3^2}\cdot\sqrt{3}=$
  Saca la raíz:
  $\displaystyle 3\cdot\sqrt{3}=3\sqrt{3}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{27}=$
3. $\sqrt{45}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \sqrt{3\cdot3\cdot5}=$
  
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \sqrt{3^2\cdot5}=$
  
  Descompone la raíz:
  $\displaystyle \sqrt{3^2}\cdot\sqrt{5}=$
  
  Saca la raíz:
  $\displaystyle 3\cdot\sqrt{5}= 3\sqrt{5}=$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{45}=$
4. $\sqrt{98}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \sqrt{2\cdot7\cdot7}=$
  
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \sqrt{2\cdot7^2}=$
  
  Descompone la raíz:
  $\displaystyle \sqrt{2}\cdot\sqrt{7^2}=$
  
  Saca la raíz:
  $\displaystyle \sqrt{2}\cdot7=7\sqrt{2}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{98}=$
5. $\sqrt{180}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \sqrt{2\cdot2\cdot3\cdot3\cdot5}=$
  
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \sqrt{2^2\cdot3^3\cdot5}=$
  
  Descompone la raíz:
  $\displaystyle \sqrt{2^2}\cdot\sqrt{3^2}\cdot\sqrt{5}=$
  
  Saca la raíz:
  $\displaystyle 2\cdot3\cdot\sqrt{5}= 6\cdot\sqrt{5}$
  $\displaystyle =6\sqrt{5}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\sqrt{180}=$
6. $\dfrac{\sqrt{8}}{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extracción parcial de la raíz
  Haz la descomposición en factores primos:
  $\displaystyle \dfrac{\sqrt{2\cdot2\cdot2}}{2}=$
  
  Búsca los exponentes pares en la descomposición:
  $\displaystyle \dfrac{\sqrt{2^2\cdot2}}{2}=$
  
  Descompone la raíz:
  $\displaystyle \dfrac{\sqrt{2^2}\cdot\sqrt{2}}{2}=$
  
  Saca la raíz:
  $\displaystyle \dfrac{2\cdot\sqrt{2}}{2}=\sqrt{2}$
  ¿Tienes una pregunta?
  Escríbelo aquí 👉
  $\dfrac{\sqrt{8}}{2}=$

Este contenido está licenciado bajo
CC BY-SA 4.0 → Información

Ejercicios con raíces cuadradas

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

Ejercicios para hacer racionales los denominadores

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

Tareas para términos con raíces cuadradas

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?

¿Tienes una pregunta?