Este curso trata sobre la introducción de las raíces cuadradas y las reglas aritméticas asociadas.

Duración: 1.5 horas aprox.

Vas a aprender:

• Definición de una raíz cuadrada

• Calcular con raíces cuadradas

• extracción parcial de la raíz

• Racionalizando el denominador

Al amigo de Carlos, el astuto Matematicus, no le gusta el enfoque de Carlos. Carlos ejectua muchos ensayos y al final se queja.

Matematicus tiene una estrategia mejor, con la que incluso la calculadora puede ayudarle.

Matematicus designa el número de cartas de un lado (cuadrado) como $kk$. Como el cuadrado tiene entonces en sus lados un número $kk$ de tarjetas, necesita un total de tarjetas $k\cdot kk\backslash cdot\; k$ para ello.

Las $4242$ cartas incluidas en el paquete se colocarán en un cuadrado con $k\cdot k=k^{2}k\backslash cdot\; k=k^2$ cartas. Por lo tanto, Matematicus establece la ecuación $k^2=42k^2=42$.

Quiere resolver esta ecuación para $kk$. La definición de la siguiente página le ayuda a hacerlo.

La raíz cuadrada $\sqrt{a}\backslash sqrt\{a\}$ es el número no negativo cuyo cuadrado da $aa$. Aquí $aa$ debe ser un número no negativo.

"No negativo" significa "positivo o $00$".

La raíz cuadrada de un número $xx$, es el número $aa$ que, al multiplicarse por sí mismo da $xx$.

Supongamos que $xx$ es $55$, entonces $aa$ es $25.25.$ La raíz cuadrada de $2525$ es $55$, porque:

El símbolo que se utiliza para indicar la raíz "$\sqrt{}\backslash sqrt\{\}$"se llama radical.

El número o la expresión que está dentro del radical se llama radicando. En la expresión $\sqrt{4}\backslash sqrt\{4\}$, el $44$ es el radicando.

Cuando el radical tiene un número $xx$, es una raíz cuadrada y se denota $\sqrt{x}\backslash sqrt\{x\}$.

Ejemplo

$\sqrt{4}=2\backslash sqrt\{4\}=2$ , puesto que $2^2=42^2=4$

Puedes encontrar más ejemplos en la siguiente página.

Como aprendiste en la definición, $aa$ es un número no negativo. A continuación, veremos algunas soluciones de raíces simples sustituyendo $aa$ por los números 9$,\frac{1}{16},\backslash frac\{1\}\{16\}$ y $00$ :

$\sqrt{9}=3\backslash sqrt\{9\}=3$ , puesto que $3^2=93^2\; =\; 9$

$\text{}\sqrt{\frac{1}{16}}=\frac{1}{4}\text{}\backslash sqrt\{\backslash frac\{1\}\{16\}\}=\backslash frac\{1\}\{4\}$ , puesto que $(\frac{1}{4}){\text{}}^2=\frac{1}{16}(\backslash frac\{1\}\{4\})^2\; =\; \backslash frac\{1\}\{16\}$

$\sqrt{0}=0\backslash sqrt\{0\}=0$ , puesto que $0^2=00^2\; =\; 0$

Así que, en general, podemos resolver una ecuación raíz de la forma $\sqrt{a}=x\backslash sqrt\{a\}=x$ cuando $a\ge 0a\ge 0$. ¿Cómo se ve cuando la raíz es negativa?

$a<0\backslash textcolor\{009999\}\{a\backslash lt0\}$ :

Por ejemplo, elegimos $a=-4a=-4$:

Buscamos un número $xx$ para el que podamos escribir como arriba:

$\sqrt{-4}=x\backslash sqrt\{-4\}=x$, puesto que $x^2=-4x^2\; =\; -4$

Si multiplicas cualquier número racional $xx$ por sí mismo, siempre obtienes un número positivo o $00$. Por lo tanto, no hay ningún número que puedas sustituir por $xx$ para que la afirmación $x^2=-4x^2=-4$ sea verdadera.

Si quieres calcular la raíz de un cuadrado, puedes poner la base en valor absoluto.

$\sqrt{a^2}=\mathrm{\mid }a\mathrm{\mid }\backslash sqrt\{a^2\}=|a|$

Sabes por la definición que una raíz cuadrada no puede ser negativa.

En este caso también puedes usar números negativos para $aa$, porque al potenciar sólo los números positivos o los que resultan al resolver una raíz cuadrada.

Por definición, el resultado de una extracción de raíz no es un número negativo. Para evitarlo, usa el valor absoluto $\mathrm{\mid }\cdots \mathrm{\mid }\backslash vert\backslash cdots\backslash vert$. Con el valor absoluto todos los números que puedes insertar serán positivos.

Como habrás notado, ya hemos aplicado esta regla a los ejemplos anteriores.

$\sqrt{9}=\sqrt{3^2}=3\backslash sqrt\{9\}=\backslash sqrt\{3^2\}=3$

Sin embargo, cuando una raíz es cuadrada, sacar el valor absoluto no es necesario:

¿Por qué puedes omitir sacar el valor absoluto aquí?

La solución ($(\sqrt{a}{)}^2=\mathrm{\mid }a\mathrm{\mid }(\backslash sqrt\{a\})^2=\backslash vert\; a\backslash vert$ también sería correcta, pero de acuerdo con la definición de la raíz cuadrada, sólo se pueden usar números racionales positivos. Como no se permite usar números negativos para la $aa$, usar el valor absoluto no es necesario.

Carkis y Matematicus asisten a la misma clase. Como tarea, los dos deben resolver la siguiente ecuación usando la raíz cuadrada:

Por la noche ambos hablan de la tarea.

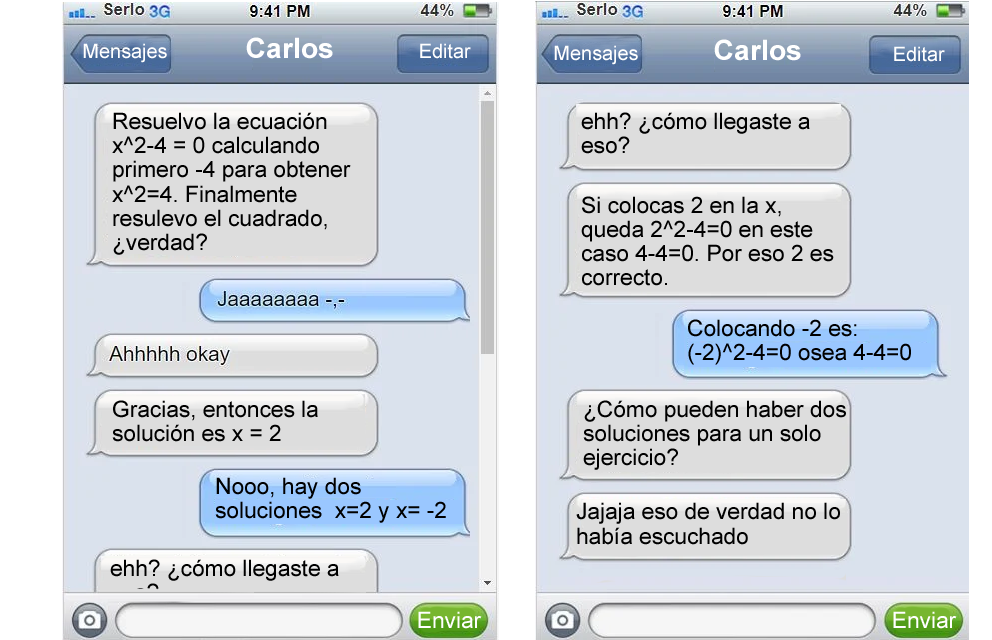
¿Quién tiene razón?

Matematicus tiene razón.

Por lo tanto, la solución correcta al problema es:

$x^2-4=0x^2-4=0$

para que de cero la $x^{2}x^2$ debe dar 4

$x^2=4x^2\; =\; 4$

Reemplazamos la $xx$ por el $44$ y la colocamos en un radical.

$\sqrt{x^2}=\sqrt{4}\backslash sqrt\{x^2\}=\backslash sqrt\{4\}$

Aquí se usa la regla de que los el valor absoluto se determina cuando el fijarse cuando el simbolo del radical está al cuadrado.

$\mathrm{\mid }2\mathrm{\mid }=2\backslash vert2\backslash vert=2$

$x_1=2;x_2=-2x\_1\; =\; 2;\; x\_2=-2$

(alternativa: $x=\pm 2x=\backslash pm2$)

Importante:

En algunos ejercicios hay que tener en cuenta el contexto de la pregunta. En algunos casos el concepto del que estámos hablando en el ejercicio se usa en otras áreas también.

Ejercicio 1

Ejercicio 2

Adición y sustracción de raíces

Adición de raíces

$c\sqrt{a}+d\sqrt{a}=(c+d)\sqrt{a}c\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}+d\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}=(c+d)\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}$

Sustracción de raíces

$c\sqrt{a}-d\sqrt{a}=(c-d)\sqrt{a}c\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}-d\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}=(c-d)\backslash sqrt\{\backslash textcolor\{ff6600\}\{a\}\}$

Puedes ver que en estas dos leyes que se ha utilizado la inversa de la ley distributiva.

¡Importante!

Sólo se pueden restar o sumar raíces si el radicando es igual.

Entonces:

Multiplicación y división de raíces

Multiplicación de raíces

$\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\backslash sqrt\{a\}\backslash cdot\backslash sqrt\{b\}=\backslash sqrt\{a\backslash cdot\; b\}$

División de las raíces

$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\backslash frac\{\backslash sqrt\{a\}\}\{\backslash sqrt\{b\}\}=\backslash sqrt\{\backslash frac\{a\}\{b\}\}$

Ejercicio 1

Ejercicio 2

Ejercicio 3

Con números de la forma $\frac{a}{\sqrt{b}}\backslash frac\{a\}\{\backslash sqrt\{b\}\}$ se puede calcular mejor si se transforma la fracción. Hay que asegurarse de que no hay ninguna raíz (es decir, ningún número real) en el denominador.

Para ello se amplía la fracción con. Esto te da:

Ejercicio 1

Ejercicio 2

Sabes que no puedes calcular $\sqrt{8}\backslash sqrt\{8\}$ en tu cabeza. Sin embargo, hay una forma de simplificar esta expresión haciendo el radicando lo más pequeño posible.

Utilizando la ley de la raíz cuadrada para multiplicar raíces, puedes dividir la raíz en dos partes. De una de estas partes se puede tomar la raíz, la otra parte permanece sin cambios.

Puedes resolver parcialmente la raíz mediante esta descomposición y simplificar las expresiones aritméticas y los términos.

Guía paso a paso:

• Descomponer el radicando en factores primos:

• Búsqueda de exponentes pares en la descomposición:

• Descompone la raíz en dos partes.

• Obtenemos una parte en la que sólo aparecen exponentes pares (de los que se puede sacar la raíz). Y una parte de la que no se puede extraer.

• Saca la raíz en la primera parte:

• Simplifica la expresión del cálculo si es posible.

El término $2\sqrt{2}2\backslash sqrt\{2\}$ no puede simplificarse más.