Este artículo trata de un grupo de cuadriláteros especiales, los rombos.

Un rombo es a veces también llamado "diamante". Este es ....
un cuadrilátero en el que
los cuatro lados tienen la misma longitud.
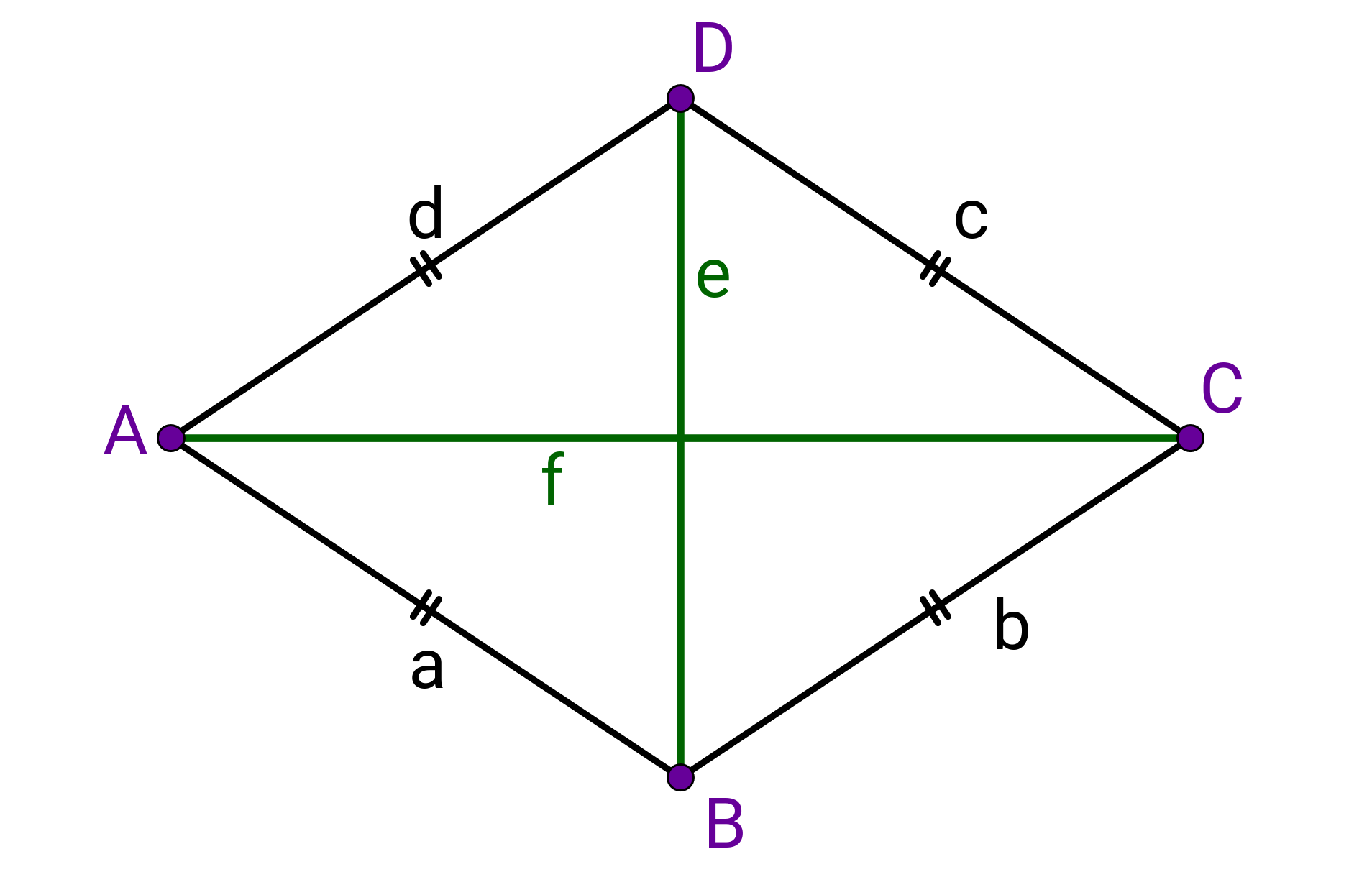
Propiedades del rombo
Características especiales para lados, ángulos y diagonales
En un rombo, los ángulos opuestos son siempre iguales.
Por tanto, para un rombo se cumple:
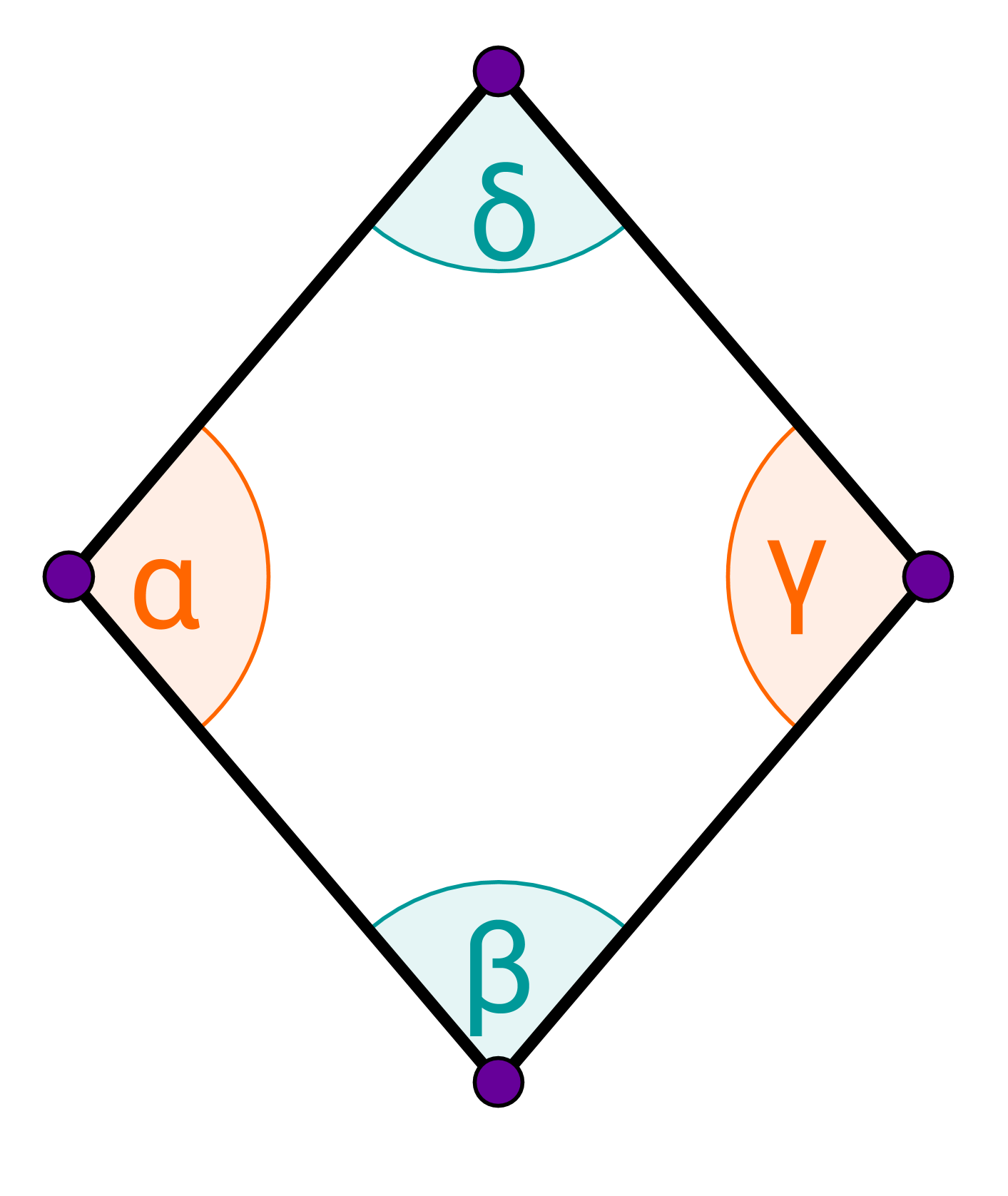
En un rombo, dos ángulos situados en el mismo lado siempre suman 180°.
Por tanto, para un rombo se cumple:
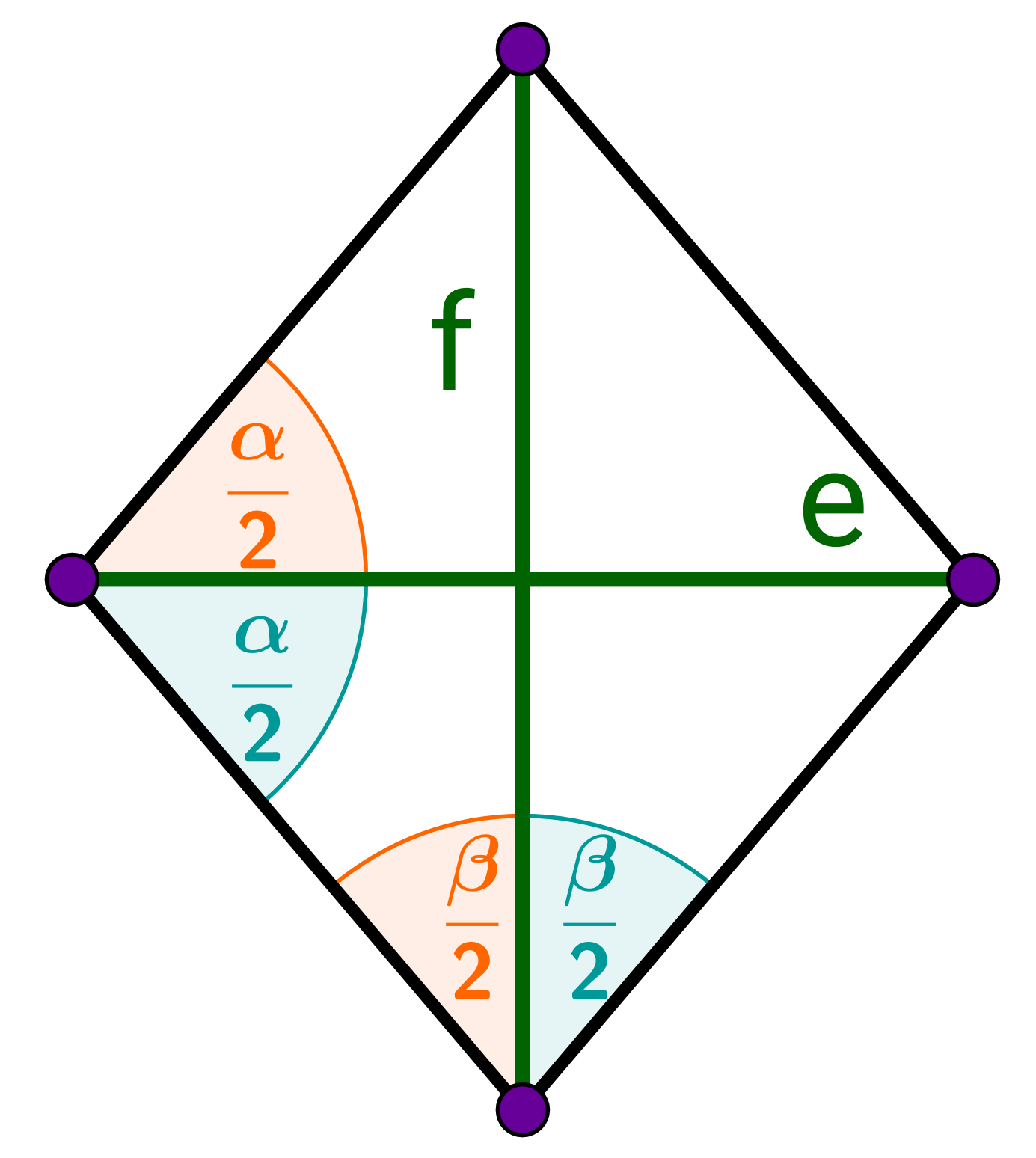
En un rombo, las diagonales se bisecan verticalmente.
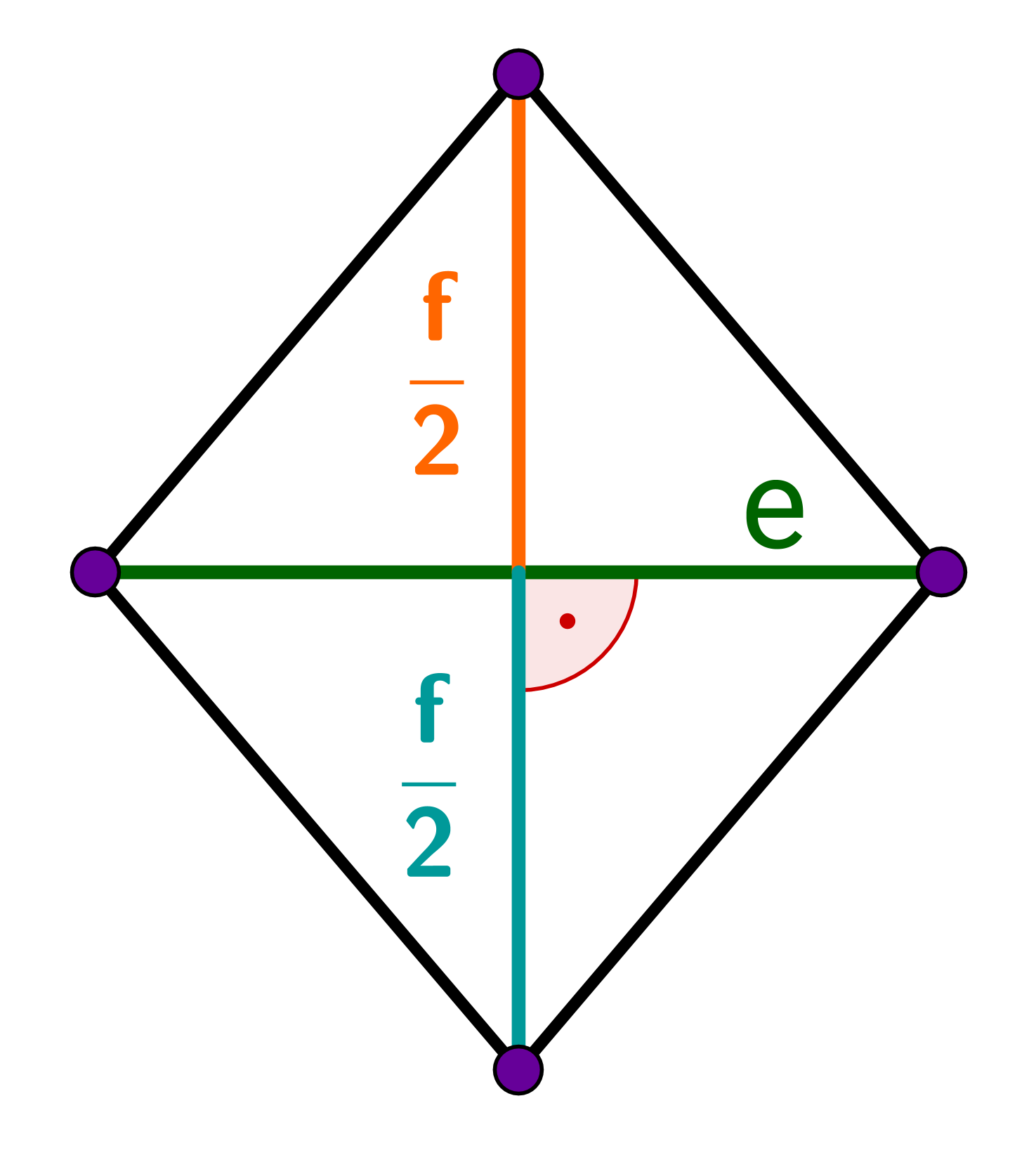
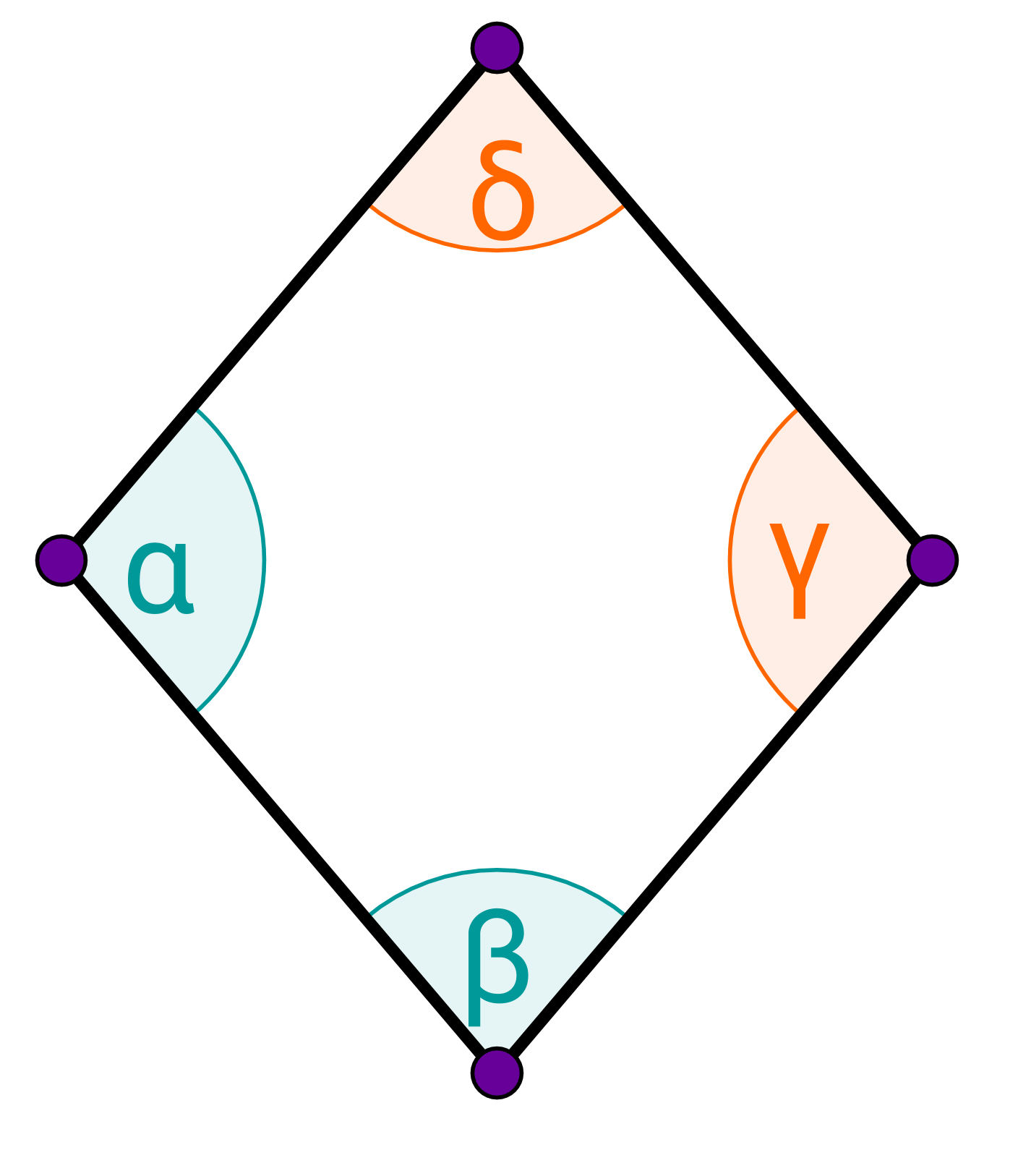
En un rombo, cada ángulo está dividido por una diagonal.
Clasificación como cuadrilátero
Todo rombo es siempre también un trapecio, específicamente un trapecio (especial) en el que no sólo un par de lados opuestos es paralelo, sino que ambos pares y además los lados son de igual longitud.
Todo rombo es siempre también un paralelogramo y un romboide, es el caso especial de estos tipos de cuadriláteros con cuatro lados de igual longitud. Un cuadrilátero es un rombo exactamente cuando es simultáneamente un paralelogramo y un romboide.
Casos especiales de rombos
Puedes ver cómo se comporta un rombo en comparación con todos los demás cuadriláteros en la Casa de los Cuadriláteros.
Propiedades de simetría
Simetría radial
Un rombo siempre tiene simetría radial al punto de intersección de las diagonales.
Siemtría axial
Un rombo tiene simetría axial con ambas diagonales como ejes de simetría.
Inscrito y Circunscrito
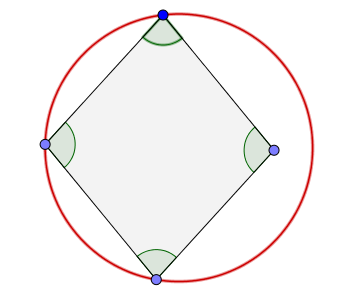
Rombo circunscrito
Un rombo generalmente no tiene circunscrito. La excepción es el caso especial en que el rombo tiene todos los ángulos rectos, es decir, es un cuadrado.
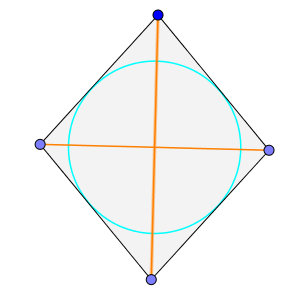
Rombo inscrito
Un rombo siempre tiene un círculo inscrito. El centro del inscrito es la intersección de las diagonales.
Área y perímetro
Área:
El área de un rombo es la mitad del producto de la longitud de ambas diagonales:
Puedes ver cómo se produce esta fórmula en el siguiente applet. Los puntos y el deslizador se pueden arrastrar.
Perímetro
El perímetro de un rombo es la suma de las longitudes de los lados. Como los cuatro lados tienen la misma longitud, el perímetro viene dado por
Still want more?
You can find more content on this topic here:
