Simetría radial - ¡Aprende con Serlo!

Una figura se tiene simetría radial cuando a través de el reflejo en espejo en un punto o en un centro de simetría la figura se refleja sobre sí misma.

Se trata de una rotación de la figura en 180°.

Figuras con simetría radial

Los puntos marcados en rojo son los puntos de simetría de las figuras.

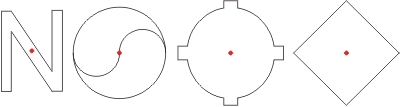
Paralelogramo

Un paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos entre sí.

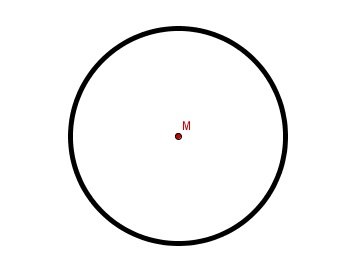
Circunferencia

Una circunferencia es una línea cerrada alrededor de un punto central $M$ . Todos los puntos de la línea tienen la misma distancia/radio al punto central.

Simetría radial en una función

La gráfica de una función es simétrica al punto $P=(x_0, y_0)$ , cuando $f(x_0-x)-y_0=-f(x_0+x)+y_0$ .

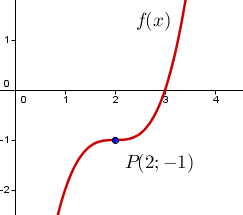
Ejemplo

La función $f(x)=(x-2)^3-1$ tiene simétria axial con el punto $P(2|-1)$ . Puesto que

$f(2-x)-(-1)=(2-x-2)3-1+1=-x^3$

y

$-f(2+x)+(-1)=-((2+x-2)^3-1) + (-1)=-(x^3-1)-1=-x^3+1-1=-x^3$

Un caso especial es la simetría puntual en el origen, es decir, para $P(0{,}0)$ . La ecuación se simplifica y se convierte en $f(0-x)-0=-f(0+x)+0\ \Rightarrow\ f\left(-x\right)=-f\left(x\right)$ .

Reflexión puntual

Para reflejar cualquier figura $F$ en un punto $P$ , todos los puntos característicos se reflejan sucesivamente en $P$ y finalmente se conectan según la forma de $F$ .

Loading