Este artículo trata de un grupo de cuadriláteros especiales llamados romboides.
Un romboide es
un cuadrilátero en el que
al menos una de sus diagonales es un eje de simetría.
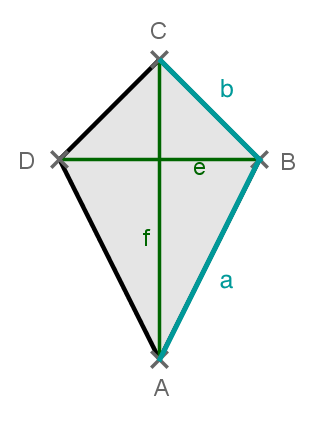
En la imagen puedes ver el ejemplo de un romboide.
En este caso, el eje de simetría es la diagonal
Definiciones equivalentes
Las diagonales son perpendiculares entre sí y una es bisectriz de la otra.
Dos lados adyacentes tienen la misma longitud.
Propiedades del romboide
Clasificación como cuadrilátero
Casos especiales de romboide
Si un romboide tiene cuatro lados de igual longitud, es un rombo.
Si un romboide tiene cuatro ángulos rectos y también cuatro lados de igual longitud, es un cuadrado.
Puedes encontrar una clasificación clara del romboide en el artículo sobre la casa de los cuadriláteros.
Propiedades de simetría
Simetría radial
Un romboide no suele tener simetría radial.
Excepción:
Un romboide tiene simetría radial si es un rombo (o un cuadrado como caso especial del rombo con cuatro ángulos rectos).
El rombo es simétrico al punto de intersección de sus diagonales.
Siemtría axial
Un romboide siempre tiene simetría axial, el eje de simetría es una de sus diagonales.
Inscrito y Circunscrito
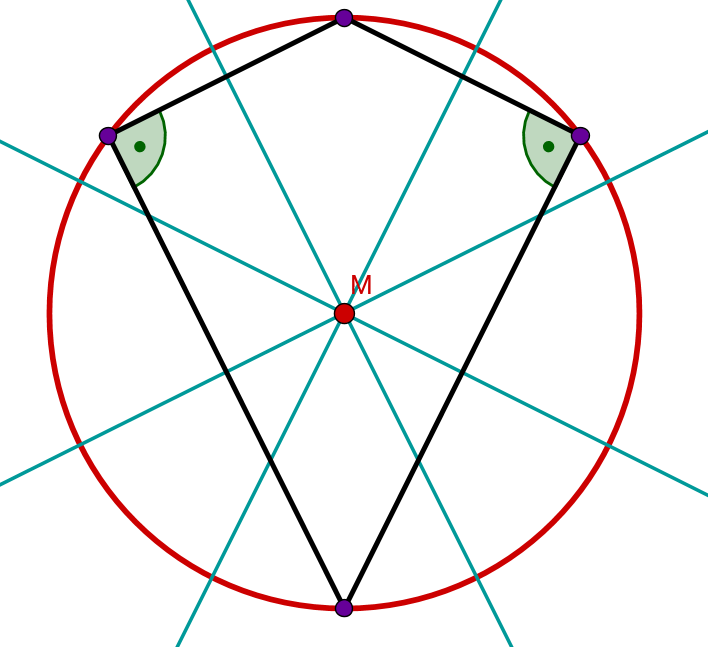
Romboide circunscrito
Un romboide generalmente no tiene circunferencia circunscrita.
La excepción es cuando los dos ángulos que no están en el eje de simetría son ángulos rectos. En este caso, el centro del círculo es el punto de intersección de las mediatrices.
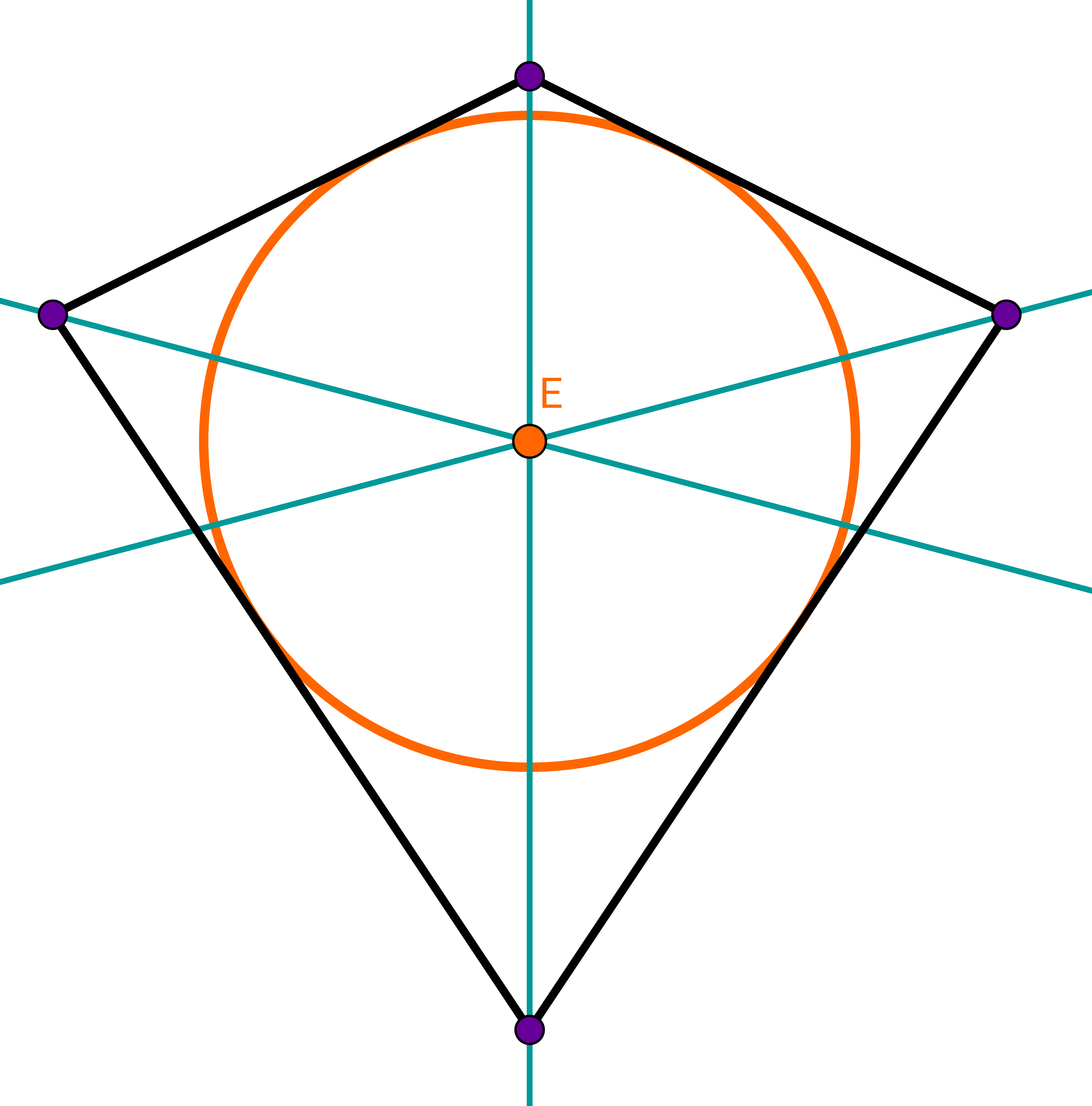
Romboide inscrito
Un romboide siempre tiene un círculo interior. El centro del círculo es la intersección de las bisectrices.
Área y perímetro
Área:
El área de un romboide es la mitad del producto de la longitud de ambas diagonales:
Puedes entender cómo se obtiene esta fórmula con la ayuda del siguiente applet:
Perímetro
El perímetro de romboide es la suma de las longitudes de los lados. Como los dos lados tienen la misma longitud, se aplica lo siguiente:
Los Romboides en la vida cotidiana
El romboide también se conoce como la cometa, un popular juguete infantil.
Still want more?
You can find more content on this topic here:
