Las fracciones están compuestas por un numerador (arriba) y un denominador (abajo), separados por un vínculo o línea de fracción horizontal:
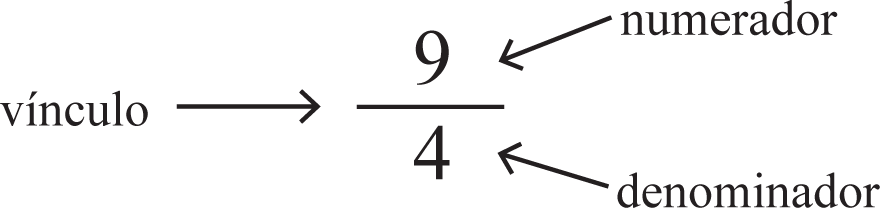
Tipos de fracciones
Se hace una distinción entre:
fracción propia (la cantidad del numerador es menor que la cantidad del denominador)
fracción impropia (la cantidad del numerador es mayor o igual que la cantidad del denominador)
fracción mixta (número entero + fracción)
fracción aparente (La fracción tiene un número entero como valor)
También ten en cuenta
fracción unitaria (el numerador es )
fracción doble (en el numerador y/o el denominador contiene una fracción dentro de la fracción)
fracción equivalente (cuando dos fracciones representan la misma parte de una unidad, es decir que tienen exactamente el mismo valor.)
Calcular con fracciones
Un resumen de las reglas para el cálculo de las fracciones se encuentraen el artículo
Se puede encontrar información más detallada en los siguientes artículos:
Para reducir y ampliar una fracción: Reduccir y ampliar una fracción.
Para calcular la suma y la resta: Adición y sustracción de fracciones.
Para calcular la multiplicación y la división: Multiplicación con fracciones y División con fracciones.
Significado de una fracción
Una fracción puede entenderse de varias maneras:
Puede expresar el tamaño de una parte o una porción de un todo (unidad).
Una fracción puede entenderse como otra anotación para un cálculo de división.
Se puede utilizar una fracción para comparar la proporción de dos números enteros entre sí.
1) Fracción para indicar el tamaño de una parte
Las fracciones pueden ser usadas para expresar que algo no se considera un todo, sino sólo una parte de un todo, y para decir cuán grande debe ser esta parte.
Ejemplo
La fracción
El círculo se dividió en partes; cada parte es un cuarto del círculo.
Si se seleccionan de las partes, son tres cuartos del círculo.

El denominador indica el número total de partes en que se ha dividido el conjunto.
El numerador indica cuántas partes se han seleccionado.
El denominador de la fracción "nombra" el tipo de partes,
el numerado "cuenta" cuántas se seleccionan.
2) Fraccion para indicar un cálculo de división
La notación fraccionaria es una forma de escritura diferente para la división, donde el numerador es el dividendo y el denominador es el divisor.
Ejemplo
Cada fracción puede ser escrita como una división y una división puede serescrita como una fracción.
De ello se deduce que cualquier número entero puede ser escrito como una fracción, asi:
3) Fracción para comparar la proporción de dos números enteros entre sí
La fracción se utiliza para indicar la proporción de dos número enteros entre sí.
De esta manera, las fracciones son una forma de indicar las proporciones. Tanto el numerador como el denominador contienen números enteros.
La razón es la comparación de dos magnitudes y se expresa mediante la división de dos números.
Ejemplo
" de las manzanas son verdes" puede indicar que " de manzanas están verdes" y igualmente también podemos decir que " de manzanas están verdes".
La cantidad de manzanas varía, pero la proporción sigue siendo la misma.
La noción de una proporción puede ser útil más adelante al ampliar las fracciones.
Laden
Importante
Sabemos que la división entre cero no es posible. Por esta razón, el denominador no puede núnca ser .
¿Por qué no?
Tenemos:
Como resultado, obtendríamos un porque
La conclusión inversa es entonces lógicamente también cierta .
Tenemos:
Asumiendo que la solución de sería un número . Entonces se aplicaría lo siguiente: .
Pero como cada multiplicación con resulta en de nuevo, la ecuación es errónea y no puede ser resuelta para ningún número .
Debido a que la conclusión inversa no se puede, ¡la división por cero tampoco está permitida!
Representacion gráfica con la circunferencia
Tenemos una circunferencia y usamos el ejemplo de .
El primer paso es imaginar una circunferencia llena.
Considéralo como 1, para un todo.

Este círculo está ahora dividido en 8 partes iguales.
Uno de estos "trozos de pastel" todavía tiene el tamaño de en relación con todo el círculo.
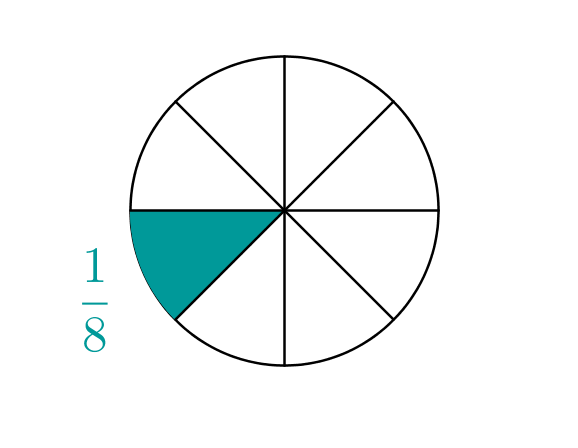
Si ahora añades 3 de estos trozos de pastel juntos, tienes
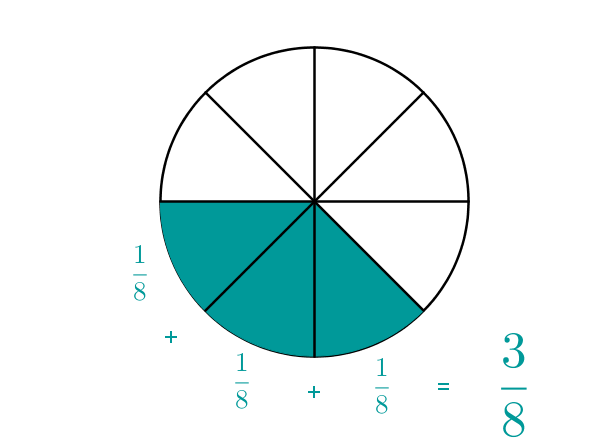
Representacion gráfica con la recta numérica
Si quieres representar fracciones en la recta numérica, debes dividirlos intervalos entre los números enteros apropiadamente.

Para la fracción , por ejemplo, se necesitan 8 secciones
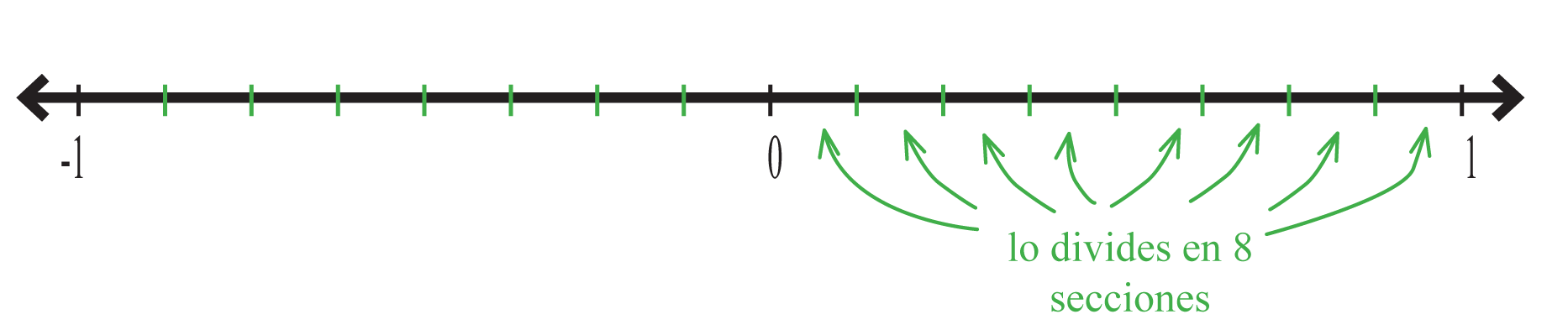
Debido a que el numerador es , la fracción se ilustra en la línea después de la tercera sección. Se pueden encontrar más ejemplos en el artículo sobrela recta numérica.

Übungsaufgaben: ¿Qué es una fracción?
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
