Productos notables: Fórmulas y operacines con binomios
Una expresión algebraica que tiene dos términos es un binomio.
Existen tres tipos de fórmulas con binomios que facilitan el uso del paréntesis y transformar una adición o una sustracción en un producto ("Factorización"). Gracias a su frecuente uso se llaman productos notables.
la primera (cuadrado de un binomio),
la segunda (cuadrado de un binomio donde su segundo término es negativo) y
el tercero (producto de dos binomios conjugados)
Las tres se dan con frecuencia y son herramientas importantes para el cálculo.
1a. fórmula: cuadrado de un binomio
Ejemplo:
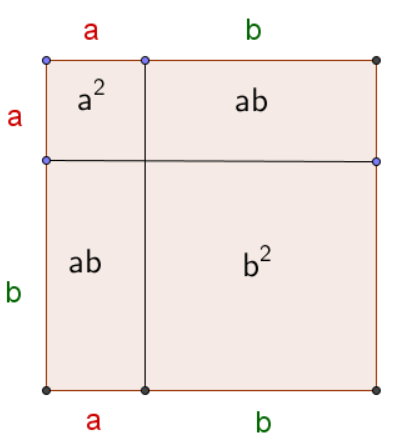
2a. fórmula: cuadrado de un binomio donde su segundo término es negativo
Ejemplo:

3a. fórmula: producto de dos binomios conjugados
Ejemplo:
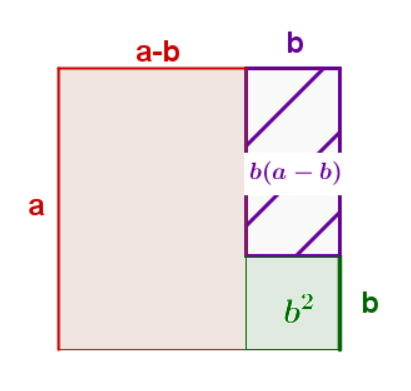
Utilización de las tres fórmulas
Las tres fórmulas con binomios se aplican en dos direcciones diferentes:
"hacia adelante" para resolver los paréntesis o
"hacia atrás" para convertir una adición o una sustracción en un producto ("Factorización").
Resolver los paréntesis - "hacia adelante"
Convierte un término del producto en una suma o resta.
Procedimiento general
Compara los términos y decide qué fórmula utilizar
Ten claro qué son y
Aplica la fórmula
Ejemplo
1a fórmula:
2a fórmula:
3a fórmula:
Factorización - "hacia atrás"
También puedes aplicar las fórmulas con binomios a la inversa. Aquí se fabrican productos a partir de sumas. Esto tiene ventajas, especialmente cuando se reduce.
Si hay tres, las dos primeras fórmulas se consideran,
Si hay dos, la tercera fórmula puede ser útil,
Si hay más de tres sumandos, primero debes intentar combinar los términos.
Tres sumandos
Si tienes tres sumandos, comprueba si dos de los sumandos son cuadrados con signo positivo. Si es necesario, primero tienes que calcular un factor adecuado usando los paréntesis. Las raíces de estos cuadrados se llaman y
Si es así, todavía hay que comprobar el término medio calculando .
Si este resultado coincide con el sumando medio del problema, puedes utilizar la fórmula con binomio para la factorización, fijándote ahora en el signo y utilizando la primera o la segunda fórmula con binomio, según corresponda.
Dos sumandos
Si tienes dos sumandos, comprueba si hay un signo menos delante de uno solo de los dos sumandos.
Si es así, comprueba si los dos sumandos son cuadrados. Si también es así, puedes factorizar con la ayuda de la tercera fórmula con binomio.
Si ninguno de los sumandos es un término cuadrado, puedes intentar sacar un factor adecuado usando el paréntesis.
Ninguna de las opciones funciona
El término no se puede factorizar con la ayuda de una fórmula con binomio. Aquí sólo puedes simplificar completando el cuadrado, pero ya no es una factorización.
El árbol de decisión correspondiente tiene este aspecto:
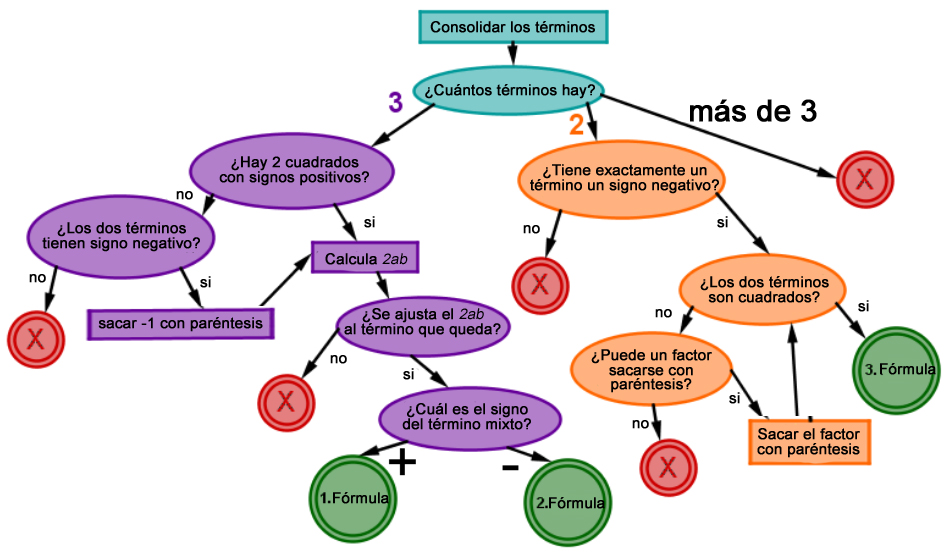
Ejemplo 1
Nada puede ser excluido/sumado y tenemos tres sumandos.
Hay 2 términos cuadrados: y
Ambos tienen un signo positivo.
Comprueba el término mixto:
, por lo que el término mixto debe ser .
Esto se ajusta a la 1a fórmula con binomio con y .
Obtienes el resultado:
Ejemplo 2
Para sacar utiliza el paréntesis:
Hay 2 términos cuadrados: y
tiene un singno positivo, uno negativo.
Se puede utilizar la 3a. fórmula con binomio con y
Obtienes el resultado: .
Ejemplo 3
Saca el con el paréntesis: .
Hay 2 términos cuadrados: y
Ambos tienen un signo positivo.
Comprueba el término mixto:
, por lo que el término mixto debe ser .
Los términos no se ajustan .
No se puede usar una fórmula con binomio.
Video
Still want more?
You can find more content on this topic here: