Común denominador con variables

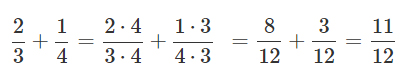
Procedimiento de cálculo

Los bloques de construcción son los factores de los denominadores. Obtienes el denominador principal multiplicando los bloques de construcción. Al hacerlo, utilizas bloques de construcción que aparecen en varios denominadores sólo una vez.

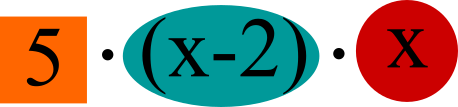
Las dos fracciones se amplian de modo que sus denominadores contienen los mismos elementos. Así las fracciones tienen un denominador común.

Ejemplos

Ejemplo 1

${\displaystyle \frac{1}{x}}+{\displaystyle \frac{2}{x+2}}\backslash dfrac\{1\}\{x\}+\backslash dfrac\{2\}\{x+2\}$

Los "bloques de construcción" aquí son:

• [$xx$]

• [$x+2x+2$]

Obtienes el común denominador como el producto de los bloques de construcción. Primero comprueba si los bloques de construcción aparecen dos veces. Si un componente aparece dos veces, sólo lo necesitas una vez.

Denominador principal: $[x]\cdot [x+2][x]\; \backslash cdot\; [x+2]$

Recursos

Como los bloques de construcción de los denominadores a menudo no son directamente visibles, utiliza primero las siguientes herramientas: factorizar y reducir la fraccion.

Ejemplo 2

Consideremos ahora una igualdad con fracciones.

${\displaystyle \frac{1}{x^2+3x}}={\displaystyle \frac{4}{5x}}\backslash dfrac\{1\}\{x^2+3x\}=\backslash dfrac\{4\}\{5x\}$

Factoriza, si es posible.

${\displaystyle \frac{1}{x(x+3)}}={\displaystyle \frac{4}{5x}}\backslash dfrac\{1\}\{x(x+3)\}=\backslash dfrac\{4\}\{5x\}$

Al factorizar, obtienes esta igualdad.

Si es posible, reduce las fracciones. ¡Esto no es posible en la ecuación dada!

${\displaystyle \frac{1}{x(x+3)}}={\displaystyle \frac{4}{5x}}\backslash dfrac\{1\}\{x(x+3)\}=\backslash dfrac\{4\}\{5x\}$

Indentifica entonces los "bloques de construcción", asi:

• [$xx$]

• [$x+3x+3$]

• [$55$]

• [$xx$]

Ejemplo 3

En el siguiente ejemplo, al igual que en el ejemplo 1, hay de nuevo un término en fracción. Ya deberías conocer las operaciones con binomios para ello.

${\displaystyle \frac{1}{x}}+{\displaystyle \frac{5}{x^2}}+{\displaystyle \frac{x+1}{x^2+2x+1}}\backslash dfrac\{1\}\{x\}+\backslash dfrac\{5\}\{x^2\}+\backslash dfrac\{x+1\}\{x^2+2x+1\}$

Factoriza, si es posible.

Aplicando las operaciones con binomios se obtiene esta ecuación:

${\displaystyle \frac{1}{x}}+{\displaystyle \frac{5}{x^2}}+{\displaystyle \frac{x+1}{(x+1{)}^2}}\backslash dfrac\{1\}\{x\}+\backslash dfrac\{5\}\{x^2\}+\backslash dfrac\{x+1\}\{(x+1)^2\}$

Ahora reduce, si es posible.

${\displaystyle \frac{1}{x}}+{\displaystyle \frac{5}{x^2}}+{\displaystyle \frac{x+1}{(x+1)}}\backslash dfrac\{1\}\{x\}+\backslash dfrac\{5\}\{x^2\}+\backslash dfrac\{x+1\}\{(x+1)\}$

Indentifica entonces los "bloques de construcción", asi:

• $[x][x]$

• $[x]\cdot [x][x]\backslash cdot[x]$

• $[x+1][x+1]$