La recta numérica

El cero $0$ divide en dos partes la recta numérica. En el lado derecho están los números positivos, en el lado izquierdo los números negativos.

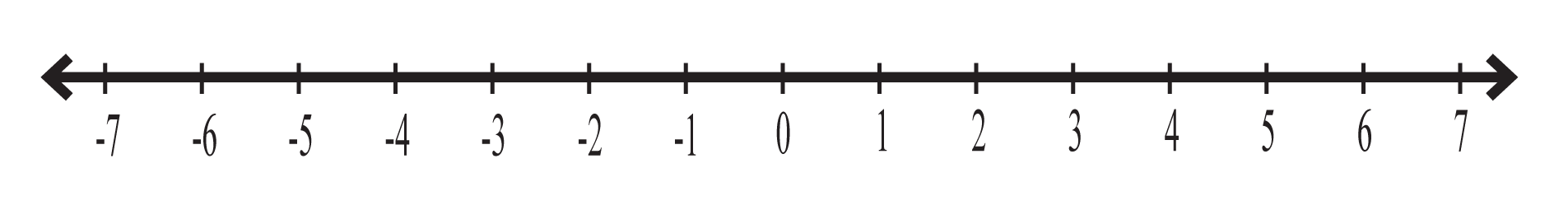
Si no necesitas números negativos, también puedes empezar la recta numérica en el 0. En este caso, la línea recta continúa sólo a la derecha y se llama rayo numérico.

Ejercicios

Ejercicio 1.

Introduce el $-1$ y $3$ en una recta numérica.

¿Qué número está en medio de los dos números en la recta numérica?

Ejercicio 2.

Introduce el $-7$ y $5$ en una recta numérica.

¿Qué número está en medio de los dos números en la recta numérica?

El punto medio también se llama el promedio.

Para calcular el punto medio utilizamos la fórmula para calcular el promedio.

Si observamos el ejercicio 2 anterior, y buscamos el promedio entre $-7$ y $5$,

• la fórmula es así:

• Simplifica la fracción:

Ejercicio 3.

Calcula el promedio entre $-15$ y $-3$.

Ejercicio 4.

Calcula el promedio entre el -25 y 15

Calculando con la recta numérica

La recta numérica también puede utilizarse para realizar adiciones y sustracciones de números enteros.

Para sumar/restar dos números, procede de la siguiente manera:

1. encontrar el primer número en la línea

2. mira el segundo número:

• Si es una adición, usas su valor para ir a la derecha.

• Si es una sustracción, ve a la izquierda.

Ejemplo:

Calcula $−2+5$.

• Identifica el  −2 sobre la recta numérica.

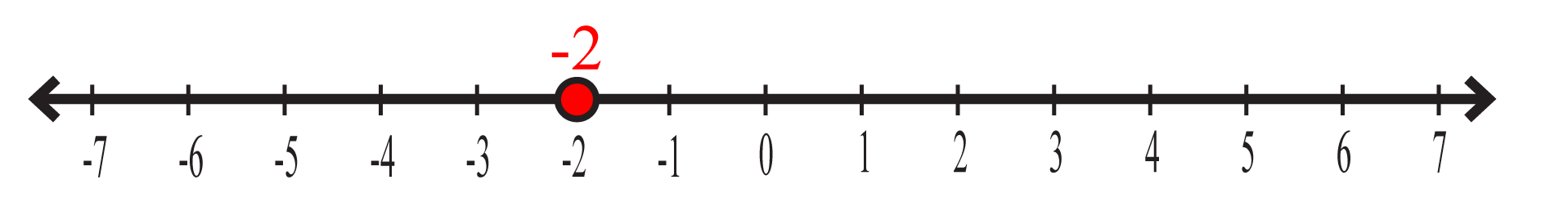
• Es una adición, así que avanza $5$ pasos a la derecha.

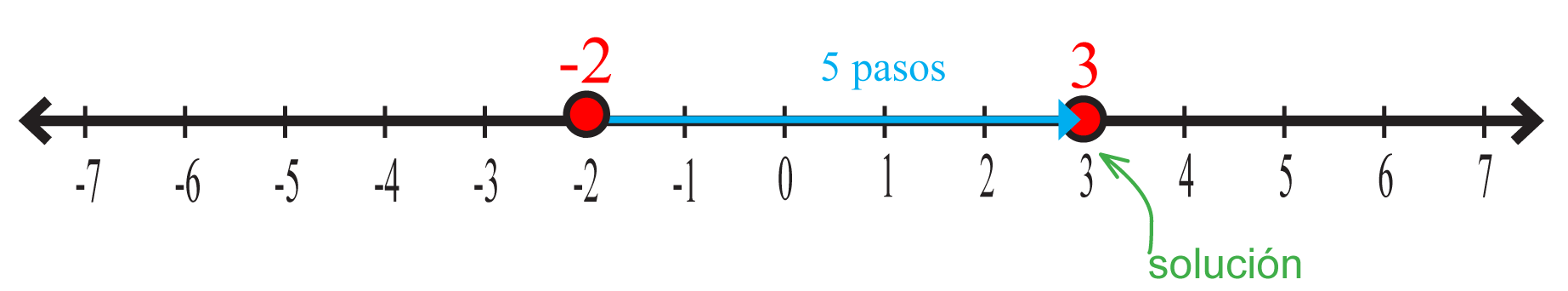
La solución es: $−2+5=3$

Ejercicios

Ejercicio 1.

Calcula $3-5$ en una recta numérica.

Ejercicio 2.

Calcula $-1+4$ en una recta numérica.

Ejercicio 3.

Calcula $-2-1$ en una recta numérica.

La recta numérica para números grandes

Para evitar tener que dibujar una recta larguísima para representar grandes números, puedes "escalar" la recta numérica. Esto significa que en lugar de marcar cada número, puedes por ejemplo marcar un punto cada 5, 10 ,100 o 1000. También puedes usar grandes escalas si sólo quieres redondear los números.

Ejemplo de una recta a escala

Por ejemplo, si quieres calcular -1000 + 4000, necesitas una línea recta muy larga. Incluso si dibujas cada unidad de sólo 1mm de largo, la recta númerica sería almenos 4000mm de largo a la derecha y 1000mm de largo a la izquierda. Eso es 5000mm en total, así que ¡sería de 5 metros!

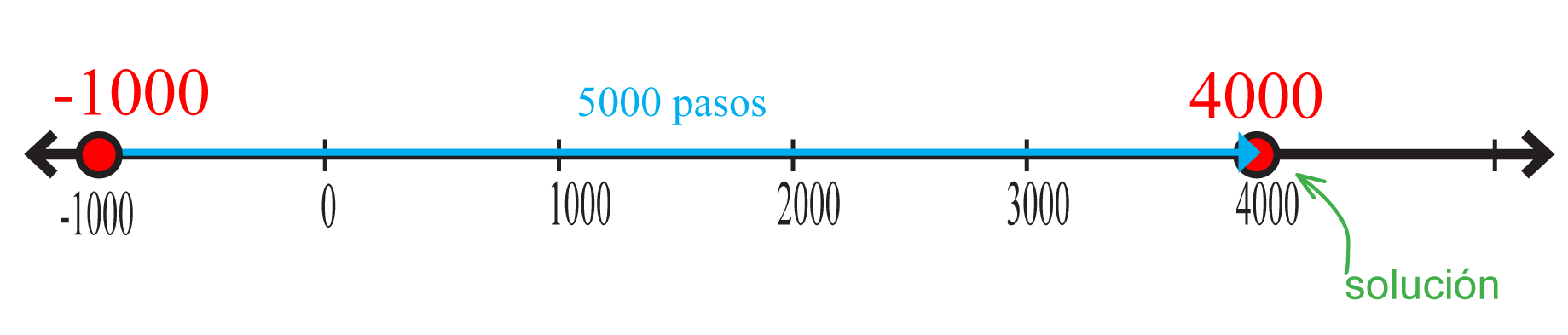
La recta numérica para fracciones

Las fracciones también pueden ser ilustradas con rectas numéricas. Para ilustrar una fracción en la recta numérica, puedes proceder de la siguiente manera:

1.     Si es una fracción mixta, converte la fracción en una fracción simple.

2.     Divide cada distancia entre dos números en partes más pequeñas. El denominador de la fracción indica en cuántas partes debe ser dividida.

3.     Observa el signo de la fracción:

• Si la fracción es positiva, desde el cero avanzas hasta elvalor del numerador a la derecha.

• Si la fracción es negativa, el valor del numerador se desplaza a la izquierdadesde el punto cero.

Ejemplo recta numérica para fracciones

Ilustra la fracción $2\frac{\text{1}}{\text{4}}$ en la recta numérica.

Tenemos esta recta numérica.

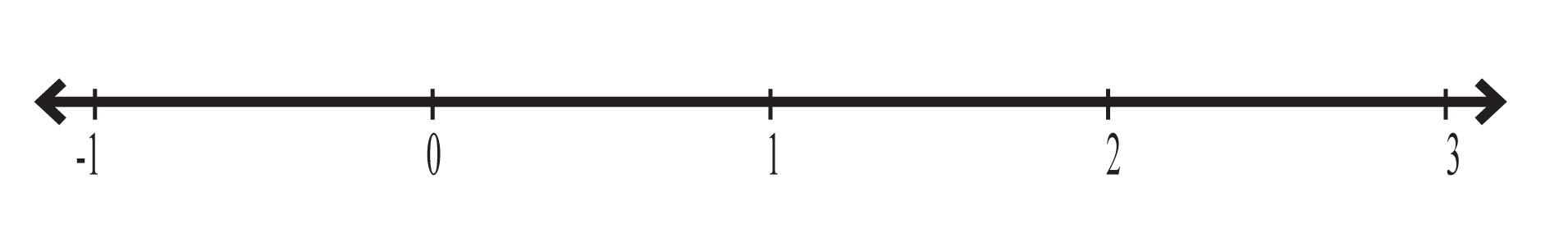
Paso 1.

$2\frac{\text{1}}{\text{4}}$ es una fracción mixta, conviertela en simple, $\frac{\text{9}}{\text{4}}$.

• Su nominador es $9$, su denominador es $4.$

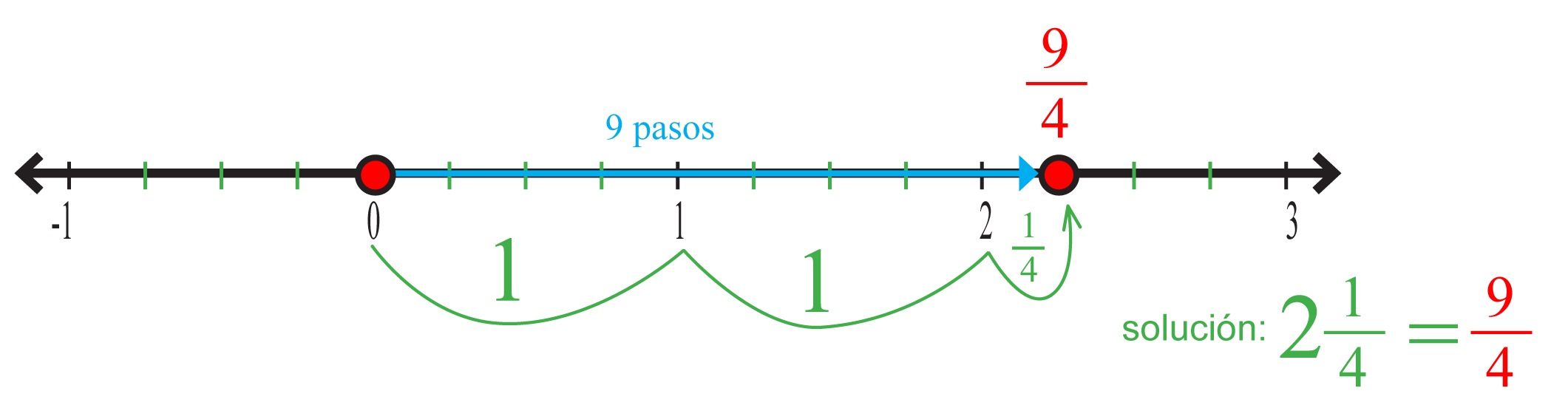
Paso 2.

Divide cada distancia entre dos números en partes más pequeñas.

El denominador de la fracción indica en cuántas partes debe ser dividida.

Para esta recta los dividimos en $4$.

Paso 3.

Observa el signo de la fracción:

• Si la fracción es positiva, desde el cero avanzas hasta el valor del numerador a la derecha. En este caso $9$ pasos.

Respuesta: $2\frac{\text{1}}{\text{4}}\ =\$$\frac{\text{9}}{\text{4}}$