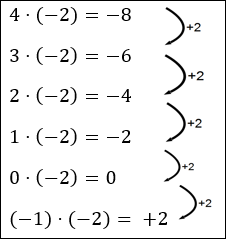1 Descripción general
Contenido del curso
En este curso se puedes aprender a calcular con números enteros. En primer lugar, la adición y la sustracción se explican con un modelo de crédito/deuda, seguidas por la multiplicación y la división.
Conocimiento previo
Deberías ser capaz de hacer toda la aritmética básica y estar familiarizado con los números enteros.
Duración del curso
El curso dura aproximadamente una hora y media.
2 El menos
Ya has tenido alguna experiencia con el signo menos "". Pero este símbolo puede ser muy diferente dependiendo de la situación. Consideremos, por ejemplo, las siguientes expresiones:
¿Qué diferencias ves entre los dos usos del menos ""?

Describe con palabras lo que podría significar la siguiente expresión:
3 Signo y elemento opuesto
Importante: El menos "" puede ser el signo para idicar que el número es negativo , también el menos "-" puede ser el símbolo para una operación aritmética de sustracción.
Si hay dos signos inmediatamente uno después del otro en un cálculo, el primero es para la operación aritmética y el segundo para determina su signo.
Símbolo para la operación aritmética
Ejemplos: o
Antes y después del símbolo hay un número.
Está ocurriendo un cálculo: restando (sustracción) o sumando (adición).
Hay un resultado (una diferencía o en tal caso una suma.)
Signo para indicar positivo o negativo
Ejemplos: ó
Cuando está justo antes del número es un signo.
El "" también puede aparecer como un signo.
Con el signo se indica si el número es positivo o negativo.
Para los números positivos generalmente el signo "" no se coloca.
Nota: para que sea mas fácil la lectura de la aritmética y los cálculos, no se colocan dos signos seguidos uno del otro. Para estos casos se utilizan los paréntesis.
Ejemplo del uso del paréntesis:
Ejercicio para diferenciar:
¿Cúal es un símbolo aritmético (operador matemático) y cuál es un signo?
4 Hallazgos
Veamos estos casos:
Ejemplo 1:
también
Cuando un y un están antes de un número, puedes reemplazarlos por un .
Ejemplo 2:
Como puedes ver, los resultados negativos como el son posibles.
Ejemplo 3:
Evidentemente esto es lo mismo que . También aplica esta regla:
Cuando un y un están antes de un número, puedes reemplazarlos por un .
Ejemplo 4:
Ejemplo 5:
Cuando un y un están antes de un número, puedes reemplazarlos por un .
5 Ejemplos con adición y sustracción
Ejemplo 1.
Calcula:
Ejemplo 2.
Calcula:
Ejemplo 3.
Calcula:
6 Multiplicación con números enteros
¿Recuerdas la relación entre la multiplicación y la suma?
Una multiplicación también puede hacerse con varias sumas. Mira este ejemplo:
"Positivo por Negativo"
Dela misma manera puedes pensar en cómo multiplicar por un número negativo:
Si lo haces de la misma manera que arriba, pueds descubrir la regla tu mismo:
Observa: El resultado no ha cambiado debido al menos (también ), pero el signo sí cambio. El resultado es ahora negativo.
"Negativo por Positivo"
Como siempre, al multiplicar, se debe aplicar lo siguiente:
Si se intercambian ambos factores, el resultado no cambia. (Ley conmutativa)
Porlo tanto, también para los números negativos se puede llegar a esta conclusión:
Regla para el cálculo
7 Número negativo por número negativo (1/2)
Ya puedes multiplicar los números negativos con los números naturales.
¿Pero cómo funciona con la multiplicación de dos números negativos?
Considera los siguientes cálculos:
Deberías ser capaz de entender estos cálculos con los conocimientos que has adquirido en el curso hasta ahora.
Ahora trata de pensar en cómo se podría continuar esta serie, y qué usarías para los dos signos de interrogación antes de hacer clic en la siguiente página del curso.
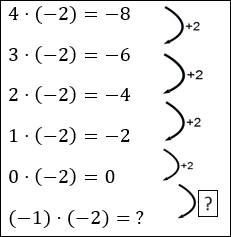
8 Número negativo por número negativo (2/2)
9 Ejemplos con multiplicación
Ejemplo 1.
Calcula:
Ejemplo 2.
Calcula:
Ejemplo 3.
Calcula:
Ejemplo 4.
Calcula:
Ejemplo 5.
Calcula:
10 División con números enteros (1/2)
Ahora que sabes multiplicar, la división ya no es difícil.
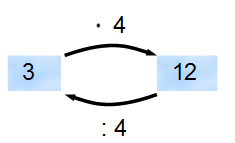
Por los números naturales sabes que
, porque .
Así que tal división es la inversa de la multiplicación.
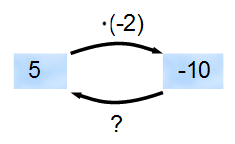
Ya sabes el resultado de la multiplicación de dos números enteros. Así que ya sabes:
.
¿Qué podrías usar para resolver el signo de interrogación en ?
Ejemplos

11 División con números enteros (2/2)
En la última página del curso vimos: | De este resultado podemos decir: | |
|---|---|---|
Negativo dividido negativo es positivo | ||
Positivo dividido negativo es negativo | ||
Negativo dividido positivo es negativo |
Al igual que con la multiplicación, esto significa:
Si cambias un signo del dividendo o del divisor, cambia el signo del cociente.
Ejemplos
Ejemplo | ||||
|---|---|---|---|---|
1. | es el cociente de los números positivos y . | |||
2. | Aquí, comparado con el ejemplo 1 en ambos casos se cambió un signo y ya el resultado es negativo. | |||
3. | Comparado con el ejemplo 2 del renglón de arriba se cambió un signo y el resultado cambia de signo también. Comparado con el ejemplo 1 del primer renglón se cambiaron ambos signos y el resultado vuelve a ser positivo. |
12 Ejemplos con división
Ejemplo 1.
Calcula:
Ejemplo 2.
Calcula:
Ejemplo3.
Calcula:
13 Resumen
Esto se aplica a todos los tipos de cálculo:
Adición y sustracción
Si y están delante del mismo número, puedes reemplazarlo con un un solo signo , así:
y
Si delante del mismo número están un y un , puedes reemplazarlo con un , así:
Multiplicación y división
"Positivo por negativo da negativo" y Negativo por positivo da negativo".
de la misma manera,
Para la división aplica: "Positivo dividido negativo da negativo" y "Negativo dividido positivo da negativo",
de la misma manera que "Negativo dividido negativo da positivo".