Raíz

Puedes sacar raíces tanto de los números como de los términos. Pero las raíces también son muy importantes a la hora de resolver ecuaciones. Sacar raíces cuadradas es la operación inversa de elevar al cuadrado.

Su cálculo

El cálculo de la raíz se denomina extracción de la raíz.

La raíz cuadrada

La raíz cuadrada de un número a es el número que tienes que elevar al cuadrado para obtener a. Es el cuadrado perfecto.

¡La raíz cuadrada de un número es siempre un número real positivo o $0$ !

La raíz cuadrada de a se escribe así:

$\sqrt[2]{a}$ o simplemente $\sqrt{a}$

El número bajo el signo de la raíz se llama radicando. Siempre es positivo o $0$ .

Ejemplos

$\sqrt{4}=2$ , porque $2^2=4$ Atención: ( $−2)⋅(−2)=4$ , pero la raíz cuadrada de un número es siempre positiva o $0$ .
$\sqrt{9}=3$ , porque $3^2=9$
$\sqrt{81}=9$ , porque $9^2=81$
$\sqrt{-3}$ no existe, porque el radicando es negativo.

Raíces de mayor orden

No sólo existe la raíz cuadrada, sino también las llamadas raíces de mayor orden. Puedes encontrar más información al respecto en el artículo sobre las raíces de mayor orden.

Raíz cuadrada de términos

Puedes sacar raíces no sólo de los números, sino también de los términos. Aquí también tienes que asegurarte de que el radicando (lo que está debajo de la raíz) no se vuelva negativo. Y al igual que con las raíces cuadradas de los números, la raíz cuadrada de los términos es siempre positiva o $0$ .

Ejemplos

$\sqrt{5x+8}$
$\sqrt{(a+2)^2}$
$-\sqrt{x-7}$

El dominio de una función - Conjunto de definición

Al sacar las raíces de los términos, tienes que asegurarte de que el radicando no se vuelva negativo. Esto significa que tienes que prestar atención al rango de definición.

Las raíces y el valor absoluto

Si hay un término bajo la raíz, tienes que tener en cuenta el valor absoluto al sacar la raíz para que siempre salga una expresión positiva.

Ejemplo 1:

$\sqrt{x^2}=|x|$

Ejemplo 2:

$\left(\sqrt{x^2}\right)=x$

Procedimiento con un ejemplo

Ejemplo: $\sqrt{6x^2}$

Procedimiento General	Con el ejemplo $\sqrt{6x^2}$
Paso 1: Primero determina el conjunto de definición del radicando.	El radicando es $6x^2$ . Éste nunca se vuelve negativo porque la variable $x$ se eleva al cuadrado y, por tanto, la expresión siempre se vuelve positiva (o $0$ ).
	El conjunto de definición es todo \mathbb{R}, es decir, todos los números positivos y negativos.

Paso 2: Sacar la raíz cuadrada y colocar las líneas de valor absoluto.

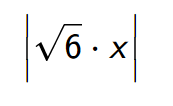
Paso 3: Considera si puedes omitir las líneas de valor absoluto.	Si se insertaran valores negativos para $x$ (están en el conjunto de definiciones), se obtendría la expresión $-\sqrt6\cdot x$ en las líneas de valor absoluto. Pero entonces la raíz cuadrada sería negativa.
Se pueden omitir si el término de las líneas de valor absoluto siempre es positivo o 0 si se utilizan todos los números del conjunto de definiciones.	Por lo tanto, no hay que omitir las líneas de valor absoluto.

Reglas de cálculo

"Racionalizar" el denominador

Si un número viene dado por $\frac{a}{\sqrt{b}}$ , entonces este número puede ampliarse con $\sqrt b$ para sacar la raíz del denominador. Los pasos del cálculo son los siguientes:

\displaystyle \frac{a}{\sqrt{b}}=\frac{a}{\sqrt{b}}\cdot\frac{\sqrt{b}}{\sqrt{b}}=\frac{a\cdot\sqrt{b}}{\sqrt{b}\cdot\sqrt{b}}=\frac{a\sqrt{b}}{b}

Extracción de la raíz en las ecuaciones

Si utilizas las raíces para simplificar las ecuaciones, ¡tienes que tener cuidado de no perder algunas soluciones! Por eso tienes que utilizar también aquí el valor absoluto.

Un ejemplo sencillo lo ilustrará:

$x^2=4 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | \sqrt{...} \;\;\; \text{Saca la raíz por ambos lados.} \\ \sqrt{x^2}=\sqrt{4}\;\;\;\;\;\;\;\;\;\;\;\; | \text{Resuelve en ambos lados según las reglas de cálculo anteriores.}\\ |2|=2 \ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |\text{Aquí es especialmente importante no olvidar el valor absoluto.}\\ \text{Ahora resuleve el valor abosuluto.}\\ x_1=2 \;\; \text{y} \;\;x_2=-2$

Si no hubieras utilizado las líneas del valor absoluto, la solución sólo habría sido $x=2$ . ¡Así que habrías perdido la solución x=-2!

Still want more?

You can find more content on this topic here:

Articles

Este contenido está licenciado bajo
CC BY-SA 4.0 → Información