Arco de círculo, sector circular y anillo circular

Circunferencia

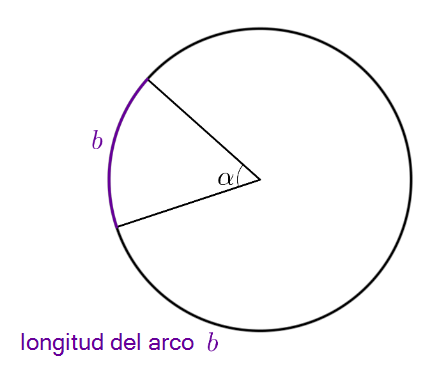
Cálculo de la longitud del arco de un círculo

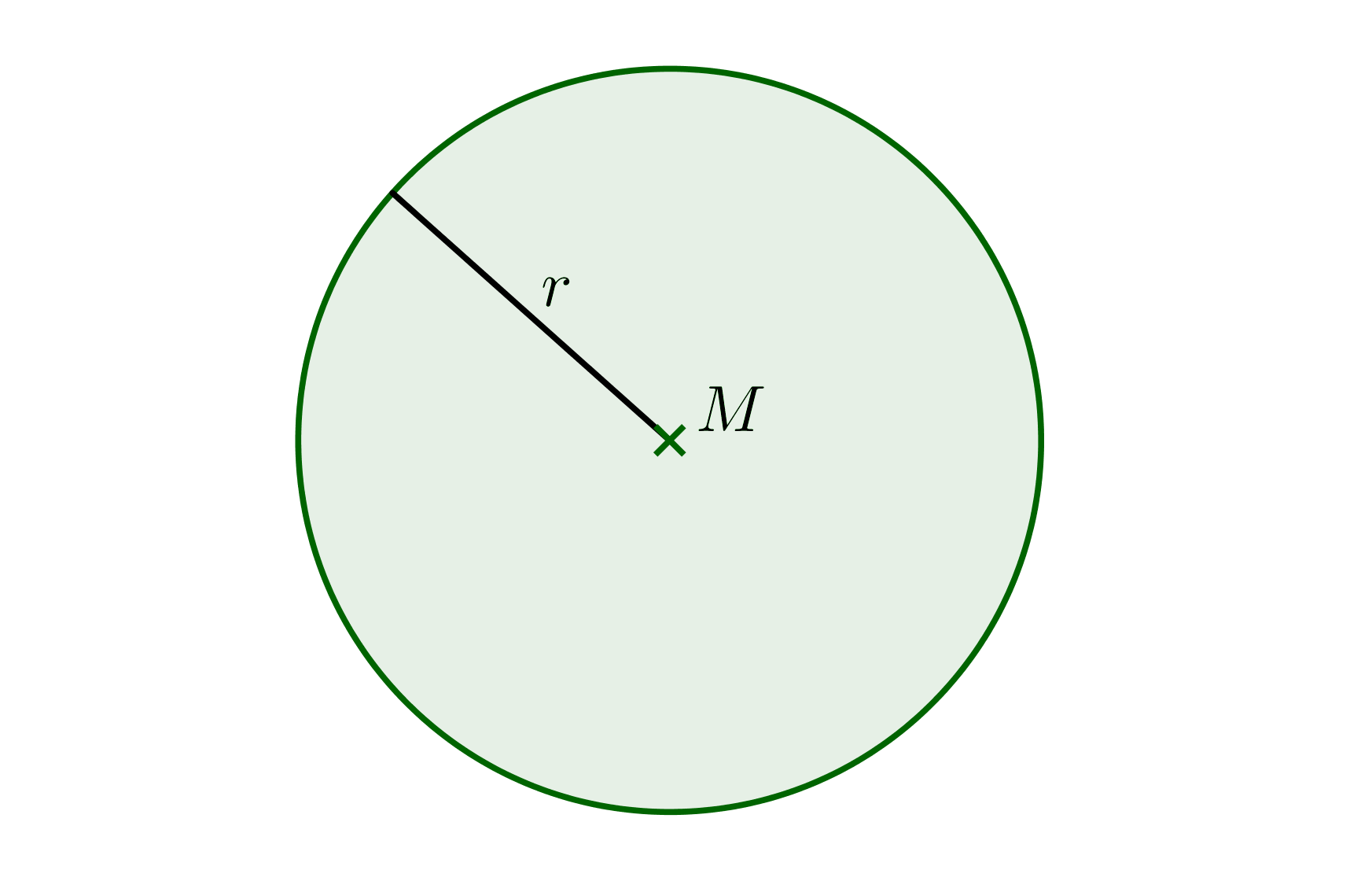
Puedes determinar la longitud del arco de un círculo b a través del ángulo $α$ incluido por el sector circular y el radio $r$ .

El círculo tiene un ángulo interno de $360^{\circ} .$

La proporción del ángulo $α$ con respecto a $360^{\circ}$ , te proporciona la fracción de la longitud del arco $b$ respecto a la circunferencia $C$ .

De esta manera, obtienes la fórmula:

$b = \frac{α}{360^{\circ}} \cdot C = \frac{α}{360^{\circ}} \cdot 2 π r$

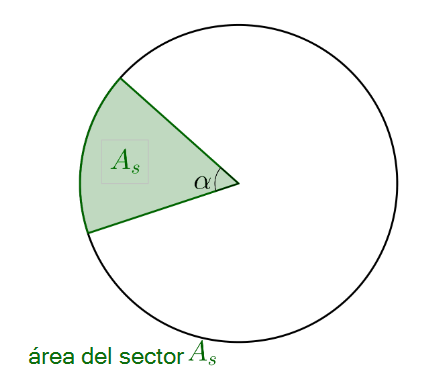
Cálculo del área del sector circular

También determinas el área del sector circular a través de la proporción del ángulo $α$ con respecto a $360 °$ . Esta relación te indica qué fracción del área del sector circular representa respecto al área total del círculo.

Entonces, la fórmula para calcular el área del sector es:

$A_{s} = \frac{α}{360^{\circ}} \cdot A_{\circ} = \frac{α}{360^{\circ}} \cdot π r^{2}$

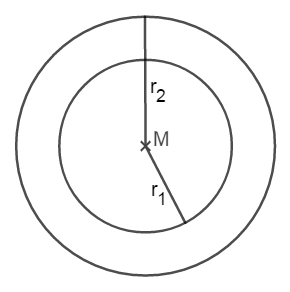
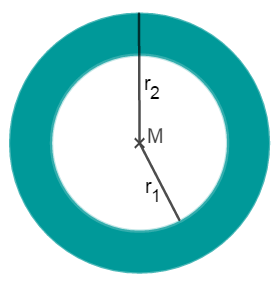
Cálculo del área del anillo circular

Un anillo circular es la área entre dos círculos con el mismo centro.

Aquí puedes ver dos círculos con el centro M.

El círculo pequeño tiene el radio $r_{1}$ , el círculo grande tiene el radio $r_{2}$ .

Calculas el área del anillo circular restando las áreas de los dos círculos entre sí:

Dos circunferencias con el mismo centro y distinto radio

$\begin{aligned} A_{anillo circular} & = A_{círculo grande} – A_{círculo pequeño} \\ = π \cdot r_{2}^{2} – π \cdot r_{1}^{2} \\ = π \cdot (r_{2}^{2} – r_{1}^{2}) \end{aligned}$

Anillo circular con radios r1 y r2 y centro M

Vídeo para el cálculo del área

Al hacer clic en la imagen o en el botón superior, aceptas que se cargará el contenido externo de YouTube . También los datos personales pueden ser transferidos a este servicio de acuerdo con nuestro Política de privacidad.

[https://youtu.be/WoNSKKLNXRY?feature=shared]

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Este contenido está licenciado bajo
CC BY-SA 4.0 → Información