Número Pi
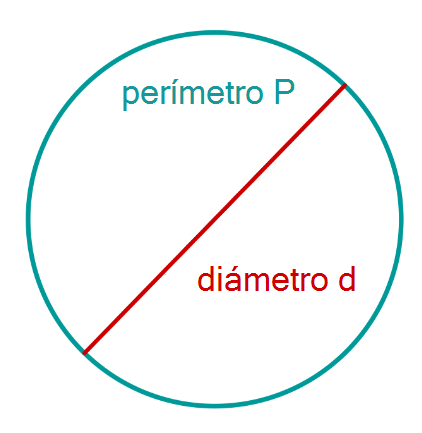
El número es una de las constantes más importantes en matemáticas. Aproximadamente es . es la relación entre la circunferencia de un círculo y su diámetro.
Se cumple: .
Ejercicios de comprensión
Construye los círculos con radio , , und y mide en cada caso la circunferencia del círculo. Crea una tabla de valores con el respectivo diámetro y circunferencia. Ingresa los pares de valores en un sistema de coordenadas, con los diámetros en el eje x y las circunferencias en el eje y. ¿Qué gráfico resulta? (ignorando imprecisiones de medición) ¿Cómo se relaciona este gráfico con la ecuación ?
Mide diámetros y circunferencias de otras formas de círculos cotidianos, como rollos de cinta adhesiva, platos, etc., y calcula sus proporciones.
Fórmulas con
Área de un círculo | |
|---|---|
Perímetro de un círculo |
La irracionalidad de
es irrational. Esto significa que no se puede expresar como una fracción de números enteros y .
Esto implica que tiene infinitas cifras decimales que no se repiten de manera periódica.
A la derecha se muestran las primeras cifras decimales de .
3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091 ...
Determinación de
Existen diversas maneras de aproximar (calculándolo cada vez con mayor precisión). Una posibilidad es el método es el de Monte Carlo:
Primero, se dibuja un círculo con radio dentro de un cuadrado con lado .
Luego, se generan puntos aleatorios en el cuadrado utilizando la computadora. (Se puede imaginar como si se dejara caer un lápiz desde una altura suficiente repetidas veces sobre una hoja de papel en la que se ha dibujado un cuadrado y un círculo).
Luego se cuenta cuántos puntos caen en el círculo y cuántos en todo el cuadrado.

En este caso, la computadora generó 999 puntos.
Si el círculo tiene radio , se aplica para el área del círculo y del cuadrado .
Das Verhältnis der zufälligen Punkte im Kreis zu den Punkten im Quadrat entspricht ungefähr dem Verhältnis der Flächen:
El resultado difiere menos del de . Si se desea un resultado más preciso, se necesitarían más puntos aleatorios.
Still want more?
You can find more content on this topic here: