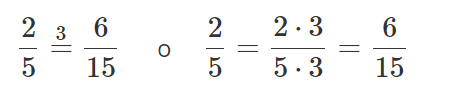3¿Qué significa ampliar?
En la sección anterior aprendiste que dos fracciones pueden describir la misma fracción. Veamos ahora con más detalle lo que esto significa.
¿Qué aspecto tiene?
La fracción coloreada en azul aquí es

Si dividimos cada parte por la mitad una vez, obtenemos

Si volvemos a dividir cada parte, entonces hay

Está claro que se mantiene:
¿Qué significa eso matemáticamente?
Si multiplicamos el numerador () y el denominador () de la fracción por el número obtenemos la fracción :
Del mismo modo, obtenemos multiplicando el numerador () y el denominador () de por cada uno:
Formalmente, podemos escribir esto como:
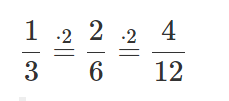
Este procedimiento se denomina "ampliar".
Descriptivamente, "ampliar" significa un refinamiento de la subdivisión,
matemáticamente, multiplicando el numerador y el denominador por el mismo número.
Importante: ¡El valor de la fracción no cambia en el proceso!
Ejemplo
Amplía la fracción con 3.
Visualmente:
Dividir las 5 partes en 3 partes iguales cada una.
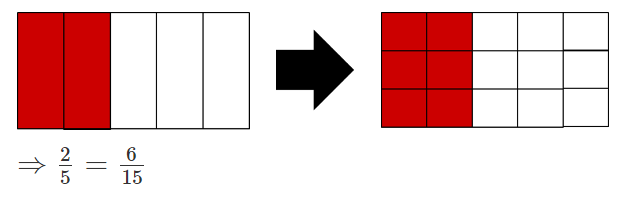
Matemáticamente:
Multiplica el numerador y el denominador por el número 3.