1 Vista general
Contenido del curso
El objetivo de este curso es conocer cómo se extienden y acortan las fracciones y cómo se utilizan para comparar tamaños.
Conocimientos previos
Debes saber lo que son las fracciones.
Duración del curso
El curso dura aproximadamente 1,5 horas (si quieres resolver todos los ejercicios por tu cuenta).
2 Fracciones diferentes con el mismo valor
Tarea
Los pizzeros Marco y Giovanni hornean pizzas del mismo tamaño. Marco divide su pizza en 6 trozos del mismo tamaño. El pizzero Giovanni, en cambio, divide su pizza en sólo 4 trozos.
Tú compras 3 trozos de pizza a Marco y tu amigo compra 2 trozos de pizza a Giovanni. ¿Quién de vosotros tiene más pizza?
Mira con atención y compara las piezas. ¿Qué notas?
¡Correcto! Ambos tienen la misma cantidad de pizza. ¿No es increíble? Tú has comprado pizzas y tu amigo y, sin embargo, los dos tienen la misma cantidad de pizza.

Veamos otro ejemplo
Tarea ¿Qué fracción es roja? Escribe como una fracción.



¿Te has dado cuenta de que la zona roja tiene siempre el mismo tamaño y, sin embargo, has utilizado diferentes fracciones para describirla?
Resumen
Para representar una misma fracción, podemos utilizar diferentes fracciones. Dicho de otra manera, a veces diferentes fracciones representan la misma fracción.
En los siguientes capítulos aprenderás más sobre esto.
3 ¿Qué significa ampliar?
En la sección anterior aprendiste que dos fracciones pueden describir la misma fracción. Veamos ahora con más detalle lo que esto significa.
¿Qué aspecto tiene?
La fracción coloreada en azul aquí es

Si dividimos cada parte por la mitad una vez, obtenemos

Si volvemos a dividir cada parte, entonces hay

Está claro que se mantiene:
¿Qué significa eso matemáticamente?
Si multiplicamos el numerador () y el denominador () de la fracción por el número obtenemos la fracción :
Del mismo modo, obtenemos multiplicando el numerador () y el denominador () de por cada uno:
Formalmente, podemos escribir esto como:
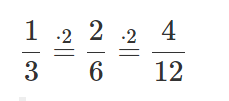
Este procedimiento se denomina "ampliar".
Descriptivamente, "ampliar" significa un refinamiento de la subdivisión,
matemáticamente, multiplicando el numerador y el denominador por el mismo número.
Importante: ¡El valor de la fracción no cambia en el proceso!
Ejemplo
Amplía la fracción con 3.
Visualmente:
Dividir las 5 partes en 3 partes iguales cada una.
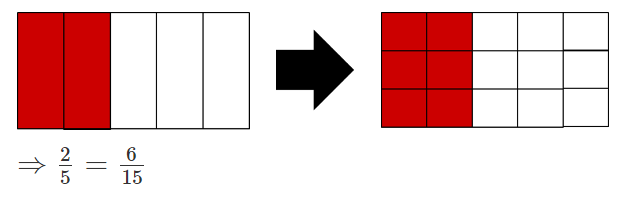
Matemáticamente:
Multiplica el numerador y el denominador por el número 3.
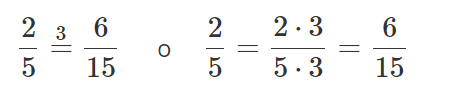
Ejercicios
Laden
4 ¿Qué significa reducir?
En el capítulo anterior, aprendiste que las fracciones pueden ampliarse dividiendo las fracciones en partes iguales o multiplicando el numerador y el denominador por el mismo número.
Por el contrario, podemos reducir fracciones o dividir el numerador y el denominador por el mismo número.
Ejemplo
del rectángulo son de color azul.

Si juntamos dos campos adyacentes a la vez, la fracción de color azul del rectángulo puede escribirse como .

Si volvemos a juntar los campos azules, recibimos la fracción .

Está claro que se mantiene:
Así, en lugar de multiplicar el numerador y el denominador por el mismo número, como en ampliar, podemos dividir el numerador y el denominador por el mismo número.
Aplica: y
Formalmente, podemos escribir esto como:
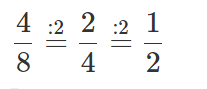
Este procedimiento se denomina "reducir".
Descriptivamente, "reducir" significa un aumento de la subdivisión. Matemáticamente, la división del numerador y el denominador con el mismo número.
Importante: ¡El valor de la fracción no cambia!
Ejemplo
Reduce la fracción con el número .
Visualmente:
Reduce en .
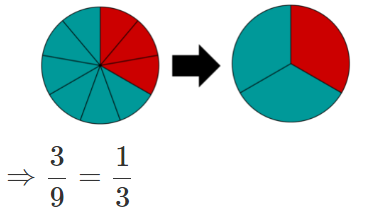
Matemáticamente:
Divide el numerador y el denominador por el número
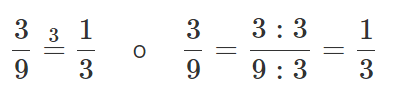
Ejercicios
Laden
5 ¿Cómo comparar el tamaño de las fracciones? 1/2
En los capítulos anteriores hemos establecido que podemos dibujar fracciones en la recta numérica. Por tanto, las fracciones siempre describen un valor numérico. Veamos ahora cómo podemos comparar este valor numérico de diferentes fracciones. Observemos la fracción de las partes rojas de los dos círculos siguientes:
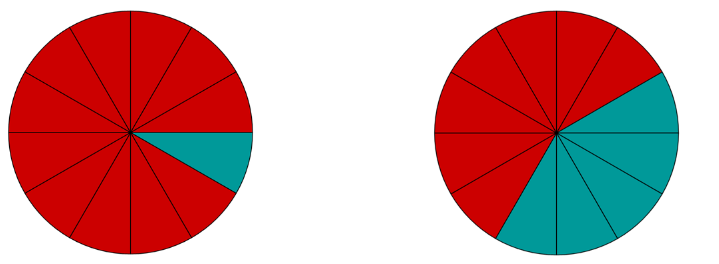
El primer círculo describe la fracción , el segundo . La primera fracción es mayor, porque tiene más partes (o trozos de pizza). Así que lo siguiente es cierto: .
Nota: Si comparas dos fracciones con el mismo denominador, la fracción con el numerador mayor es mayor.
Pero, ¿qué ocurre ahora si los denominadores no son iguales? Observemos la fracción de las partes rojas de los siguientes círculos:
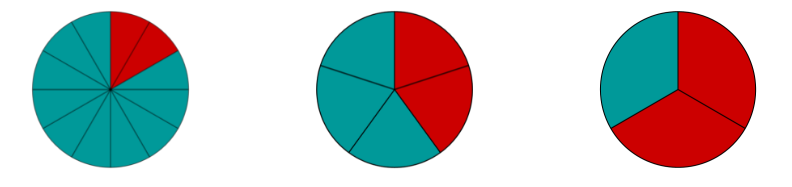
Así que esta vez comparamos las fracciones . La tercera fracción es la mayor porque las dos partes son mayores:
.
Cuantos más trozos dividamos una pizza, más pequeños serán los trozos.
Nota: Si comparas dos fracciones con el mismo numerador, la fracción con el denominador más pequeño es mayor.
En este capítulo hemos aprendido a comparar fracciones cuyos denominadores o numeradores son iguales. En el próximo capítulo veremos qué ocurre cuando ni el numerador ni el denominador son iguales.
Ejercicios
¿Cuál de las dos fracciones es mayor?
a) o
b) o
c) o
d) o
6 ¿Cómo comparar el tamaño de las fracciones? 2/2
¿Cómo podemos comparar las fracciones , y ? Nuestras reglas de la sección anterior no ayudan aquí: ni los numeradores ni los denominadores coinciden.
Sin embargo, podemos ajustar los denominadores ampliándolos y reduciéndolos.
¿Podemos ampliar las fracciones para que todas tengan el mismo denominador al final? Hemos visto en un ejercicio anterior que en este caso podemos expandir todas las fracciones al común denominador 40:
Por lo tanto, según nuestra regla general para fracciones con el mismo denominador, se deduce:
Podemos aplicar este procedimiento a cualquier fracción: Si queremos comparar fracciones que no tienen ni el mismo numerador ni el mismo denominador, debemos expandir estas fracciones a un denominador común llamado denominador principal. Para ello, determinamos el minimo común múltiplo (MCM) de los denominadores que aparecen y expandimos todas las fracciones a este múltiplo. En el ejemplo anterior, se trataba de 40, y ampliamos las fracciones en 5, 8 y 10, respectivamente.
Nota: Las fracciones sólo se pueden comparar si los numeradores o los denominadores son iguales.
Si los denominadores son iguales, la fracción con el numerador mayor es mayor.
Si los numeradores son iguales, la fracción con el denominador más pequeño es mayor.
Si ni el numerador ni el denominador son iguales, las fracciones se llevan a un denominador común, normalmente ampliandolas.
¿Cuál de las dos fracciones es mayor?
a) o
b) o
c) o
7 Ejercicios
Laden
Laden
Laden
