Potenciación
La potenciación es una notación abreviada para multiplicar un número por sí mismo varias veces.
Ejemplo: se escribe como
El exponente, en este ejemplo , describe cuántas veces se multiplica un número por sí mismo.
En general, cualquier número sin exponente tiene un exponente de .
Se aplica:
En este caso se suele omitir el exponente.
Ejemplo:
Si se eleva cualquier número a la potencia de , cuando , siempre se obtiene .
Excepción: " " no está definido.
Base y exponente
El número que se va a multiplicar por sí mismo se llama base y el número de veces es indicado por el exponente, el resultado de este cálculo es entonces la potencia.
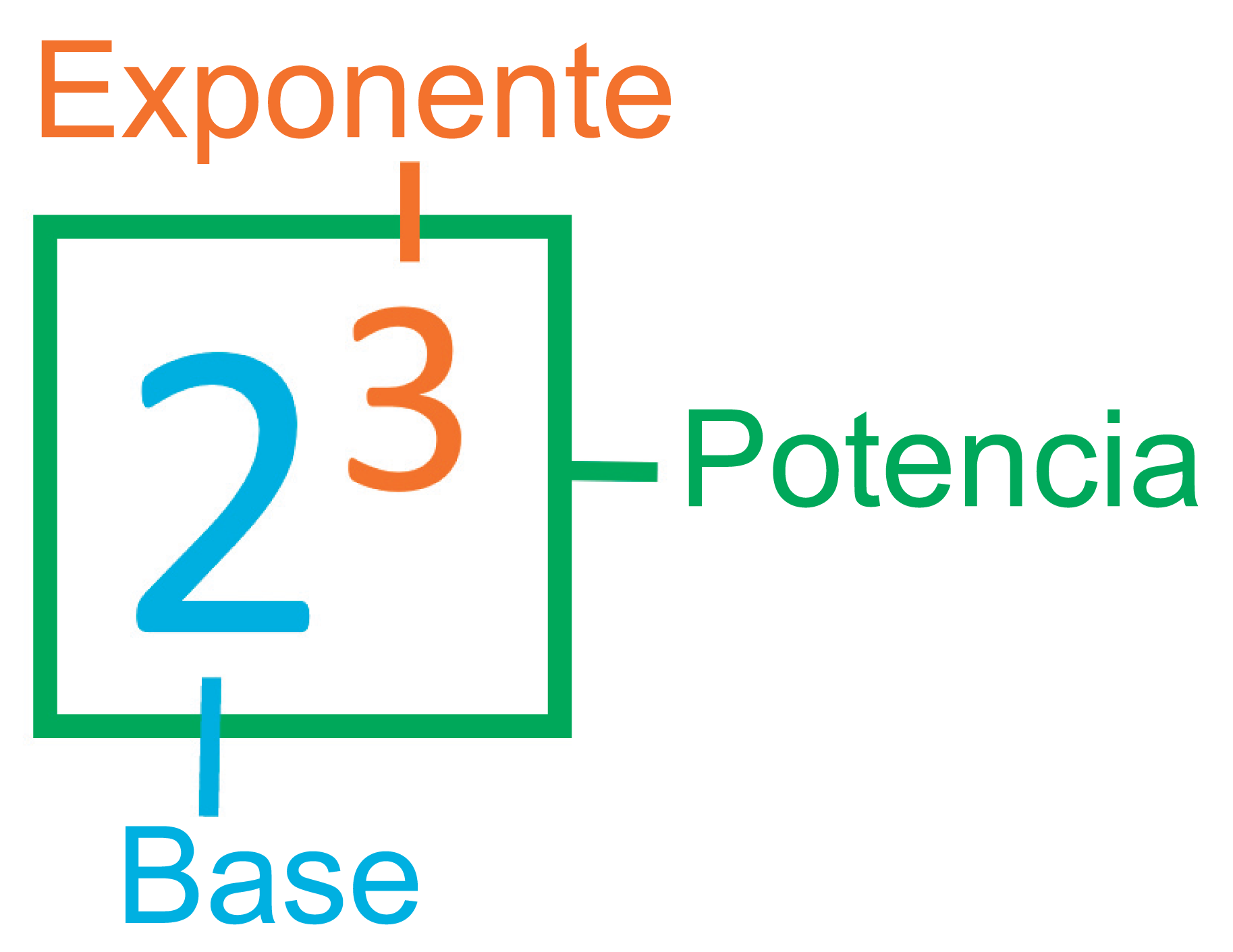
Ejemplo:
Potencias con base negativa
Si se realiza la potenciaci[on de un número negativo, el signo del resultado depende de si el exponente es un número par o impar. Si es par, el resultado es positivo; si es impar, la potencia sigue siendo negativa.
Ejemplos:
Potencias con exponente negativo
¿Cómo podemos interpretar ?
Ejemplos:
Exponentes racionales
Los números elevados a la potencia de un número racional (es decir, una fracción) pueden identificarse como una raíz:
Por lo tanto, lo contrario es cierto para la raíz estándar:
Ejemplo 1:
Ejemplo 2:
Calculando con exponentes
En el artículo Leyes de la potenciación puedes leer cómo calcular con potencias y qué Leyes de la potenciación hay.
Still want more?
You can find more content on this topic here: