Número Pi
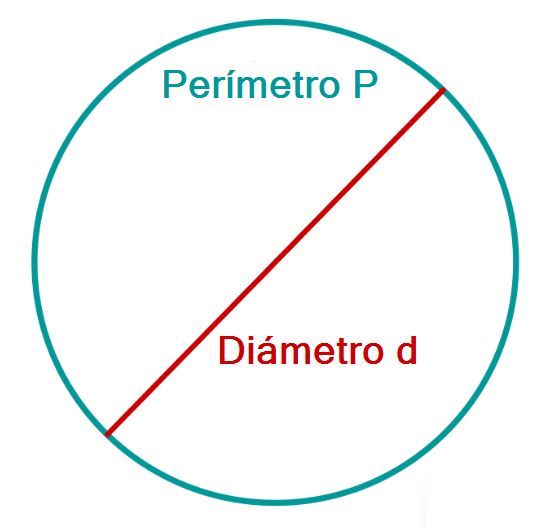
El número es una de las más importantes en matemáticas. Aproximadamente, . es la relación entre el perímetro de una circunferencia y su diámetro. Se cumple que
Ejercicios para la comprensión
Construye circunferencias con radio , , y y mide en cada caso la longitud de la circunferencia. Crea una tabla de valores con los respectivos diámetros y longitudes de las circunferencias. Representa los pares de valores en un sistema de coordenadas, con los diámetros en el eje 𝑥 y las longitudes en el eje
𝑦.
¿Qué gráfico se obtiene? (aparte de pequeñas inexactitudes en las mediciones).
¿Cómo se relaciona este gráfico con la fórmula ?
Mide el diámetro y la circunferencia de otros objetos circulares que encuentres en la vida cotidiana, como rollos de cinta adhesiva, platos, etc., y calcula su relación.
Fórmulas con
Área de un círculo | |
|---|---|
Perímetro de un círculo |
La irracionalidad de
es irracional. Esto significa que no se puede escribir como una fracción de números enteros y .
Esto implica que iene infinitas cifras decimales que no se repiten de manera periódica.
A la derecha se pueden ver los primeros decimales de .
3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091 ...
Determinación de
Existen muchas maneras de aproximar (= es decir, calcularlo con mayor precisión). Una de ellas es el método de Montecarlo.
Primero, se dibuja una circunferencia con radio dentro de un cuadrado con lado de longitud .
Luego, se hace que el ordenador genere puntos al azar dentro del cuadrado. (Puedes imaginarlo como si dejaras caer repetidamente un lápiz desde una cierta altura sobre una hoja de papel en la que están dibujados un cuadrado y una circunferencia).
Después, se cuenta cuántos puntos caen dentro de la circunferencia y cuántos en todo el cuadrado.

El ordenador ha generado 999 puntos aquí.
Si la circunferencia tiene el radio , el área de la circunferencia und vom Quadrat .
Das Verhältnis der zufälligen Punkte im Kreis zu den Punkten im Quadrat entspricht ungefähr dem Verhältnis der Flächen:
El resultado se desvía menos de de . Para obtener un resultado más preciso, se necesitan más puntos aleatorios.
Still want more?
You can find more content on this topic here: