7División: fracción dividida por fracción
A Tomás y a su amigo les quedan litros de cola. Quieren decantarlas en botellas más pequeñas y manejables. Hay espacio para litros en cada botella pequeña.
¿Cuántas botellas necesitan?
Primero, veamos un ejemplo más sencillo. Si queremos llenar litros en botellas de 2 litros, calculamos: . Así que se necesitan 10 botellas para llenar litros en botellas de litros.
Del mismo modo, ahora podemos calcular cuántas botellas necesitan Tomás y su amigo. Calculamos:
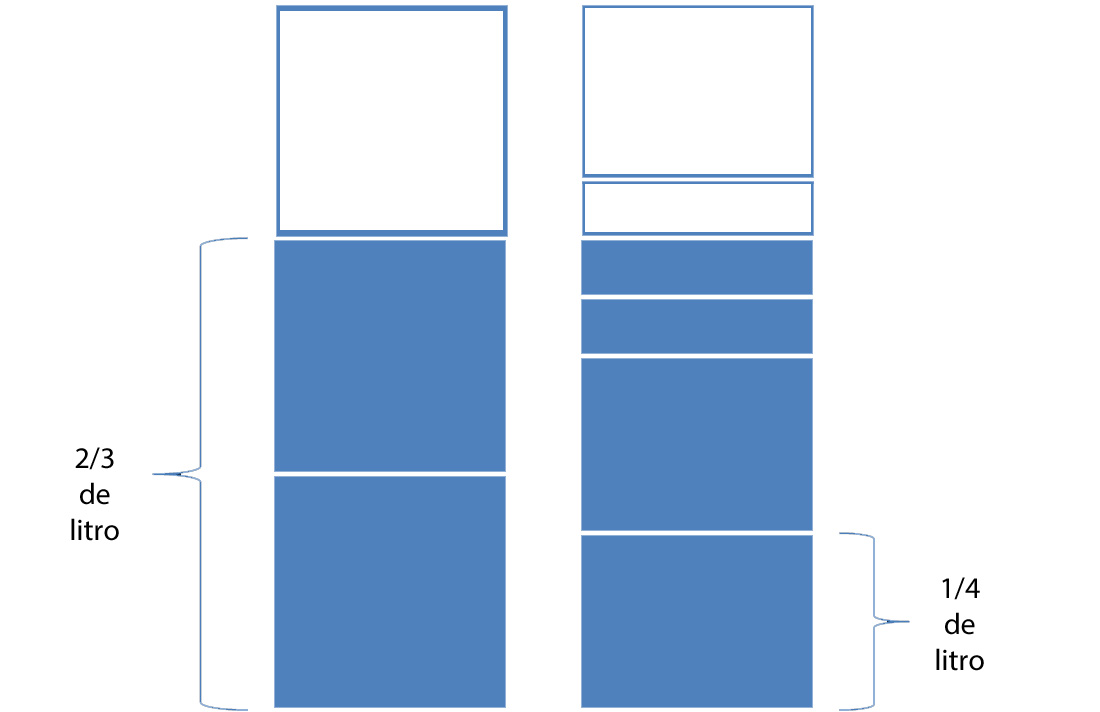
Intentemos visualizar de nuevo este cálculo. A la izquierda se ven los litros. A la derecha la misma cantidad de cola, pero en subdivisiones de litros. De esto podemos ver que Tomás y su amigo necesitan un total de botellas pequeñas. La tercera botella, sin embargo, sólo está llena hasta .
Entonces:
En el último paso, convertimos la fracción mixta.
En el capítulo anterior, aprendiste que en lugar de dividir por un número, podemos multiplicar por la fracción invertida. Lo mismo ocurre al dividir por una fracción.
Obtenemos fracción invertida de una fracción intercambiando el numerador y el denominador. Así, fracción invertida de es igual a y esta es .
Así que podemos calcular:
Nota:
Dividimos una fracción por otra multiplicando por la fracción invertida.
