Multiplicando el contenido de los paréntesis

Cuando un término que está compuesto por un paréntesis (que contiene una suma o una resta),

su contenido se debe multiplicar.

Cada sumando o en tal caso el minuendo y sustraendo se debe multiplicar con este término.

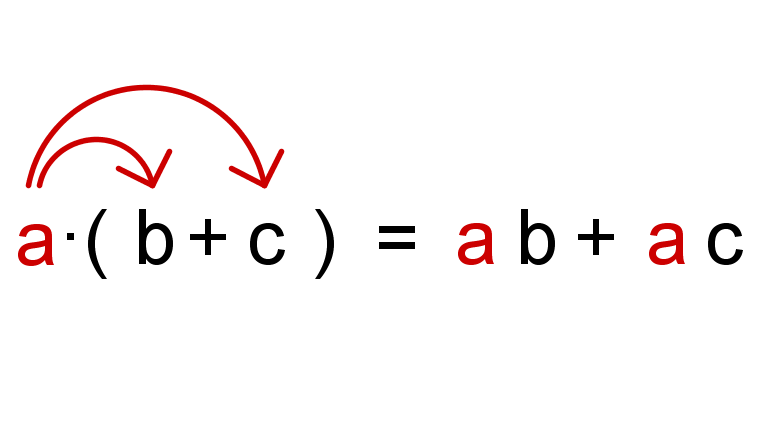
Gráfico: Multiplicando el contenido del paréntesis. “Cada sumando recibe el factor a.”

Multiplica el factor por el paréntesis

Cada elemento de la suma o diferencia en los paréntesis debe ser multiplicado por el factor que se ubica directamente antes (¡o inclusive despúes!) del paréntesis:

• Si un número debe ser multiplicado por un paréntesis que contenga una suma o diferencia, cada sumndo o en tal caso el minuendo y el sustraendo, deben ser multiplicados por este número.

• Utiliza este mismo procedimiento de multiplicar el contenido del paréntesis también cuando la variable o el término es más largo.

Ejemplos

Paréntesis por paréntesis

Si el término por el que se debe multiplicar el paréntesis es a su vez un paréntesis con una suma o resta, cada término de la primera suma o resta debe ser multiplicado por cada término de la segunda suma o resta.

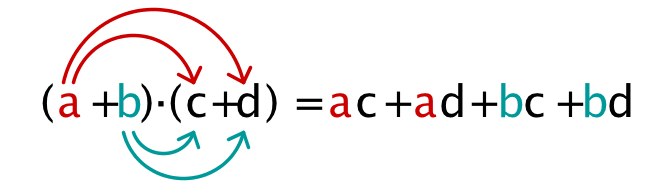
Gráfico: Multiplicando dos paréntesis. “El contenido de un paréntesis por el contenido del otro paréntesis”

Ejemplo

Si se multiplica el mismo paréntesis por sí mismo (por ejemplo, $(a+b)⋅(a+b)$ ) o se considera un término de la forma $(a+b)⋅(a-b)$, se puede simplificar el trabajo utilizando las fórmulas de binomio.

Producto entre paréntesis

Si hay un producto entre paréntesis (en lugar de una suma o diferencia), no se puede multiplicar cada factor del producto entre paréntesis por el factor anterior al paréntesis, sino sólo uno (no importa cuál).

$\rightarrow$Los paréntesis pueden omitirse según la ley asociativa, los factores pueden intercambiarse según la ley conmutativa.

$a⋅(b⋅c)=a⋅b⋅c$

Ejemplos

• $2⋅(x+y)=2x+2y$ , pero $2⋅(x⋅y)=2xy≠2x⋅2y=4xy$

• $0{,}5⋅(x⋅6y)=0{,}5x⋅6y=3xy$   o también:  $0{,}5⋅(x⋅6y)=x⋅3y=3xy$