Sistemas de valor posicional

Los sistemas de valor posicional son sistemas numéricos que funcionan según el principio de agrupación. A cada dígito de un número se le asigna un valor. Los sistemas de valor posicional más conocidos son el sistema decimal y el sistema binario.

Historia

Antes de que existieran los números, la gente escribía los números utilizando diferentes símbolos, como guiones o puntos. Así que para escribir 5 ovejas, escribían 5 guiones: ||||| o también puntos: $\cdot \cdot \cdot \cdot \cdot . ⋅⋅⋅⋅⋅.$

Cuanto más grandes sean los números, más confuso será este sistema. También tiene otras limitaciones. Por ejemplo, no es posible o es muy incómodo representar números negativos o fracciones.

Fuente Imágen: Wikimedia Commons

Con la ayuda de los sistemas de valor posicional, es más fácil representar los números y realizar cálculos complicados.

Diferentes sistemas de valor posicional

Hay artículos detallados sobre los siguientes sistemas de valor posicion

Sistema decimal

El sistema decimal representa los números en base 10 y es nuestro sistema de numeración cotidiano.

Sistema binario y sistema hexadecimal

Los sistemas binario y hexadecimal representan números de base 2 y 16 respectivamente. Se utilizan hoy en día en la tecnología y el procesamiento de datos.

Conceptos básicos

Los sistemas de valor posicional proporcionan dos informaciones de un vistazo, ya que el propio dígito y el lugar donde está colocado revelan algo:

la posición o lugar en el que se coloca el dígito revela la unidad de su agrupación,
la cifra revela el la cantidad de agrupaciones.

Quieres expresar el número de puntos azules en un número.

Paso 1: ¡Ordena!

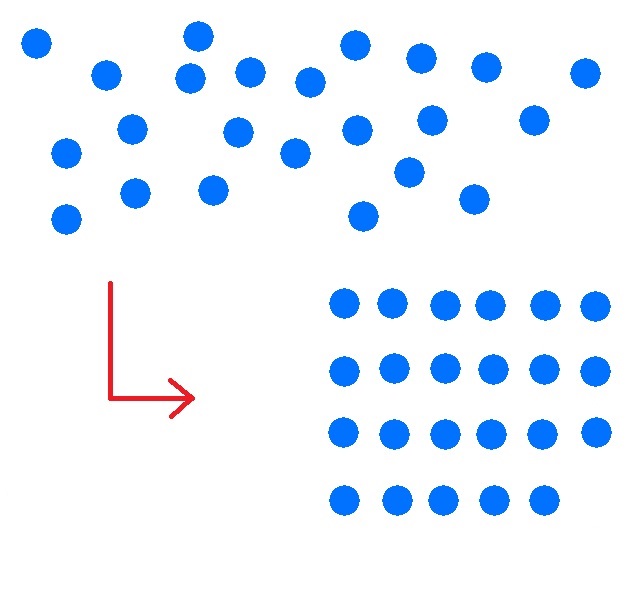
Paso 2: ¡Agrupa!

Combina siempre 5 puntos en un paquete.

Nota: Grupos de 5 puntos indica que estamos calculando en base 5.

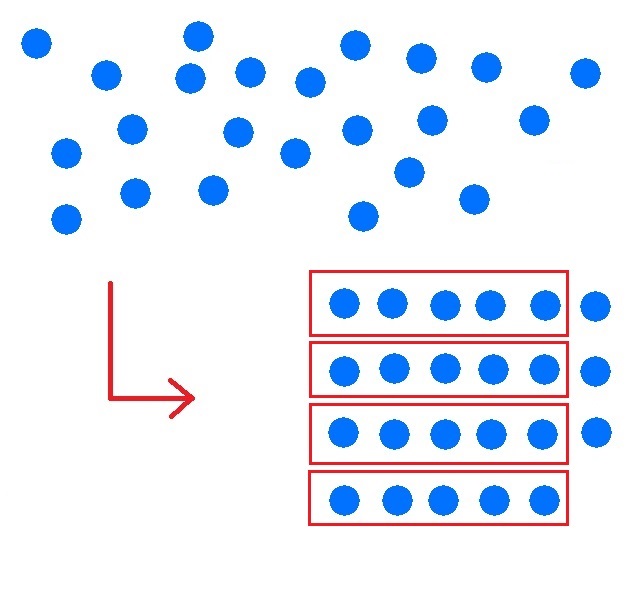
Paso 3: ¡Cuenta!

Cuenta 4 paquetes y 3 puntos simples.

Anota primero el número de paquetes y luego el número de puntos sueltos.

Como siempre se agruparon 5 puntos en un paquete, "43" sale como número, aunque hay 23 puntos. Para conseguir el conocido valor 23, tendrías que agrupar siempre diez puntos en un paquete.

El cero

Para poder describir todos los números con este modo que usa agurpaciones (paquetes), habría que pensar en un "marcador de posición" que dijera, por ejemplo, que no hay puntos individuales, sino sólo conjuntos. Este marcador de posición es el cero.

Ahora que se ha inventado el cero: "Cuatro paquetes de diez y ni un solo punto" podría escribirse como $40$ .

Porque todo el mundo sabe que cuando el 4 está en el segundo lugar de la derecha, describe decenas.

Conceptos y notación

Base: La base describe el número de puntos que se agrupan en un paquete. En el ejemplo de la derecha, la base sería $6$ .

Cifras: Si la base de un sistema es b, hay exactamente $b$ cifras en ese sistema. Así, en el ejemplo de la derecha tenemos en cuenta 6 cifras: 0, 1, 2, 3, 4 y 5.

Posicion y valor posicional: El lugar de una cifra se llama posición. A cada posición se le asigna un valor posicional. Este valor posicional es $\textcolor{ff6600}{b^\text{ digito de posición}}$ , por lo que los dígitos se numeran de derecha a izquierda empezando por el $0$ . Por tanto, los tres primeros valores de posición en base seis son $\textcolor{ff6600}{6^0}$ , $\textcolor{ff6600}{6^1}$ y $\textcolor{ff6600}{6^2}$ .

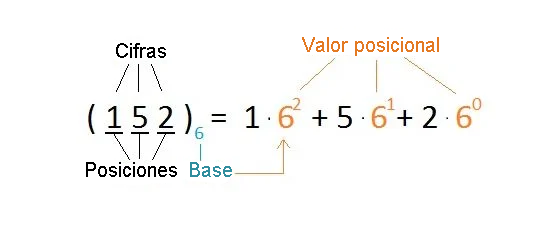
Para dejar claro en qué sistema de valor posicional se expresa un número, se utiliza un índice que indica la base:

$(43)_5=(23)_{10}=23$

$(152)_6=(68)_{10}=68$

La base 10 significa que estás en el sistema decimal.

Tablero de valor posicional

En una tabla de valor posicional, los valores posicionales se escriben en la primera línea para que los dígitos del número puedan escribirse debajo.

El número $(1032)_{4}$ por tanto, tendría esta tabla de valores.

valores posicionales		$4^{3}$	$4^{2}$	$4^{1}$	$4^{0}$
		$1$	$0$	$3$	$2$

En el sistema decimal, también se escribe M, C, D, U,... para las unidades, decenas, centenas,... en la primera línea.

Así que puedes introducir el número $1032$ :

Símbolo de valor posicional		M	C	D	U
Valor		$10^{3}$	$10^{2}$	$10^{1}$	$10^{0}$
Cifra		$1$	$0$	$3$	$2$

Si quieres introducir decimales, añade d,c,m,... para décimas, centésimas, milésimas,...

Símbolo de valor posicional		M	C	D	U	,	d	c	m
Valor		$10^{3}$	$10^{2}$	$10^{1}$	$10^{0}$	,	$10^{-1}$	$10^{-2}$	$10^{-3}$
Cifra		$1$	$0$	$3$	$2$	,	3	5	0

El número sería entonces $1032,350$

Cambia de sistema de valor posicional

Puedes representar los números en diferentes sistemas de valor posicional.

Ejemplos:

Ejemplo 1: Representa el número 31 en base 5.

Puedes imaginar 31 puntos que están ordenados y que ahora quieres agrupar en cinco.
¿Cuántos paquetes de cinco tienes?

Calcula $31:5=6\ R1$

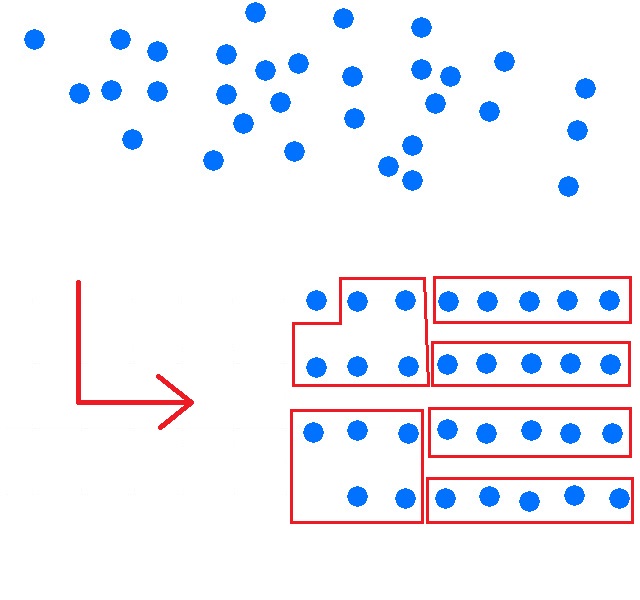
$\Rightarrow6$ paquetes de cinco y $1$ punto único.

$\Rightarrow 31=6\cdot5^1+1\cdot5^0$

Ahora los seis paquetes deben agruparse de nuevo en cinco, ya que el número 6 no existe en el sistema quíntuple.

Calcula $6:5=1\ R1$

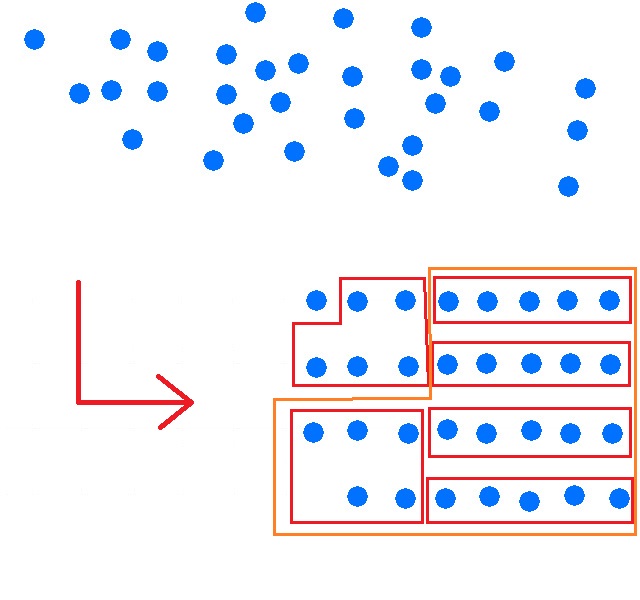
$\Rightarrow1$ paquete de cinco grupos de cinco puntos y $1$ grupo único de cinco y 1 punto.

$\Rightarrow 31$ puntos

$=1\cdot5^2+1\cdot5^1+1\cdot5^0$

= $(111)_{5}$

Produce un total de:

1 paquete color naranja,

1 grupo color rojo,

1 punto.

Ejemplo 2: Coloca el número $(615)_{7}$ en la base 4.

Procedimiento:

Paso 1: Escribe $(615)_{7}$ como una suma y calcula: $(615)_7=6\cdot7^2+1\cdot7^1+5\cdot7^0\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=294+7+5\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=306$
Paso 2: Divide $306$ en $4$ $306:4=76 \,\,\,\textcolor{ff6600}{R2}$
Paso 3: Divide $76$ en $4$ $76:4=19 \,\,\,\textcolor{ff6600}{R0}$
Paso 4: Divide $19$ en $4$ $19:4=4 \,\,\,\textcolor{ff6600}{R3}$
Paso 5: Divide $4$ en $4$ $4:4=1 \,\,\,\textcolor{ff6600}{R0}$
Paso 6: Divide $1$ en $4$ $1:4=0 \,\,\,\textcolor{ff6600}{R1}$ Como el resultado de la división es $0$ , hemos terminado aquí. Los restos R son ahora las cifras para las valores de posición. El primer resto que hemos calculado pertenece al valor posicional $4^{0}$ el segundo a $4^{1}$ etc. $306=\textcolor{ff6600}{1}\cdot4^4+\textcolor{ff6600}{0}\cdot4^3+\textcolor{ff6600}{3}\cdot4^2+\textcolor{ff6600}{0}\cdot4^1+\textcolor{ff6600}{2}\cdot4^0=(\textcolor{ff6600}{10302})_4$

Exercises: Sistemas de valor posicional

You can find more exercises in the following folder::
Sistema decimal

Still want more?

You can find more content on this topic here:

Articles

Sistema decimal

Este contenido está licenciado bajo
CC BY-SA 4.0 → Información