Números complejos: Introducción

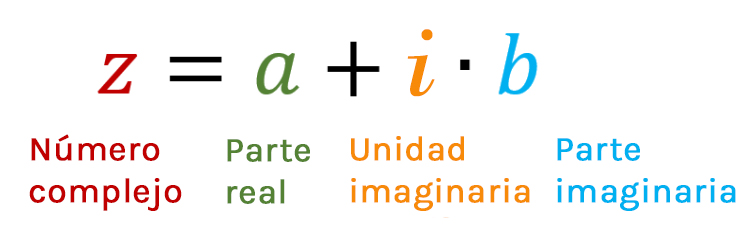
¿Qué son los números complejos?

La ecuación $x^2+1=0$ no tiene solución en los números reales que conoces hasta ahora. Sin embargo, si hubiera un número que elevara $-1$ al cuadrado, la ecuación podría resolverse. No existe tal número en los números reales $ℝ$. Por tanto, introducimos el conjunto numérico de los números complejos $ℂ$.  

Con eso puedes resolver la ecuación anterior: $x=\pm i.$

Ejemplos

• $z_1=4+3i$ y $z_2=\frac{1}{2}+\frac{3}{5}i$ son números complejos. Entonces, puedes sustituir cualquier número real en $a$ y $b$, y obtendrás un número complejo. Para $z_1$, la parte real es $4$ y la parte imaginaria es $3$. Para $z_2$, la parte real es $\frac{1}{2}$ y la parte imaginaria es $\frac{3}{5}$.

• También $z_3=5i$ es un número complejo. En este caso, $a=0$ y $b=5$. Por lo tanto, $\text{Re}(z_3)=0$ e $\text{Im}(z_3)=5$.

• $z_4=4$ es un número real, pero también es un número complejo. En este caso, $a=4$ y $b=0$. Por lo tanto, $\text{Re}(z_4)=4$ e $\text{Im}(z_4)=0$.

Los números reales son un subconjunto de los números complejos.

Los números reales $ℝ$ son un subconjunto de los números complejos $ℂ$. Esto significa que cada número real también es un número complejo, pero no todos los números complejos son números reales.

De manera similar, por ejemplo, los números naturales $\mathbb{N}$ son un subconjunto de los números reales $ℝ$. Cada número natural es también un número real, pero no todos los números reales son números naturales. Por ejemplo, el número natural $4$ es también un número real, pero el número real $\mathrm{2,67}$ no es un número natural.

Términos importantes

Es decir, se sustituye el más del medio por un menos.

El valor absoluto también se suele representar con la letra $r$.

Con el número complejo conjugado también se cumple: $z\cdot \overline{z}={\left|z\right|}^2$

Ejemplos

La cantidad conjugada compleja de $z_1=3+4i$ se obtiene al reemplazar el signo más por un signo menos. Por lo tanto, la cantidad conjugada compleja es $\overline{z_1}=3-4i$.

¿Cuál es el número complejo conjugado de $z_2=2-i$? Aquí no hay un más, sino un menos en el centro. Sin embargo, puedes reescribir $z_2$: $z_2=2-i=2+(-i)$.

Ahora puedes cambiar el más por un menos para formar los complejos conjugados:

$\overline{z_2}=2-(-i)=2+i$

Calcula además los valores absolutos de: $z_1,\overline{z_1}$ y $z_2$:

Para $z_1=3+4i$ es $a=3$ y $b=4$. Lo colocas en la fórmula para el valor absoluto:

$|z_1|=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$

Para $z_1=3+4i$ es $a=3$ y $b=-4$. El valor absoluto es entonces:

$|\overline{z_1}|=\sqrt{3^2+(-4{)}^2}=\sqrt{9+16}=\sqrt{25}=5$

Para $z_2=2-i$ es $a=2$ y $b=-1$. El valor absoluto es entonces::

$|z_2|=\sqrt{2^2+(-1{)}^2}=\sqrt{4+1}=\sqrt{5}$

Sigue con los siguientes temas:

• Números complejos: Adición y sustracción de dos números complejos

• Números complejos: Multiplicación de dos números complejos

• Números complejos: Dividir dos números complejos

• Números complejos: Representación de los números complejos en el sistema de coordenadas