¿Qué es una función?
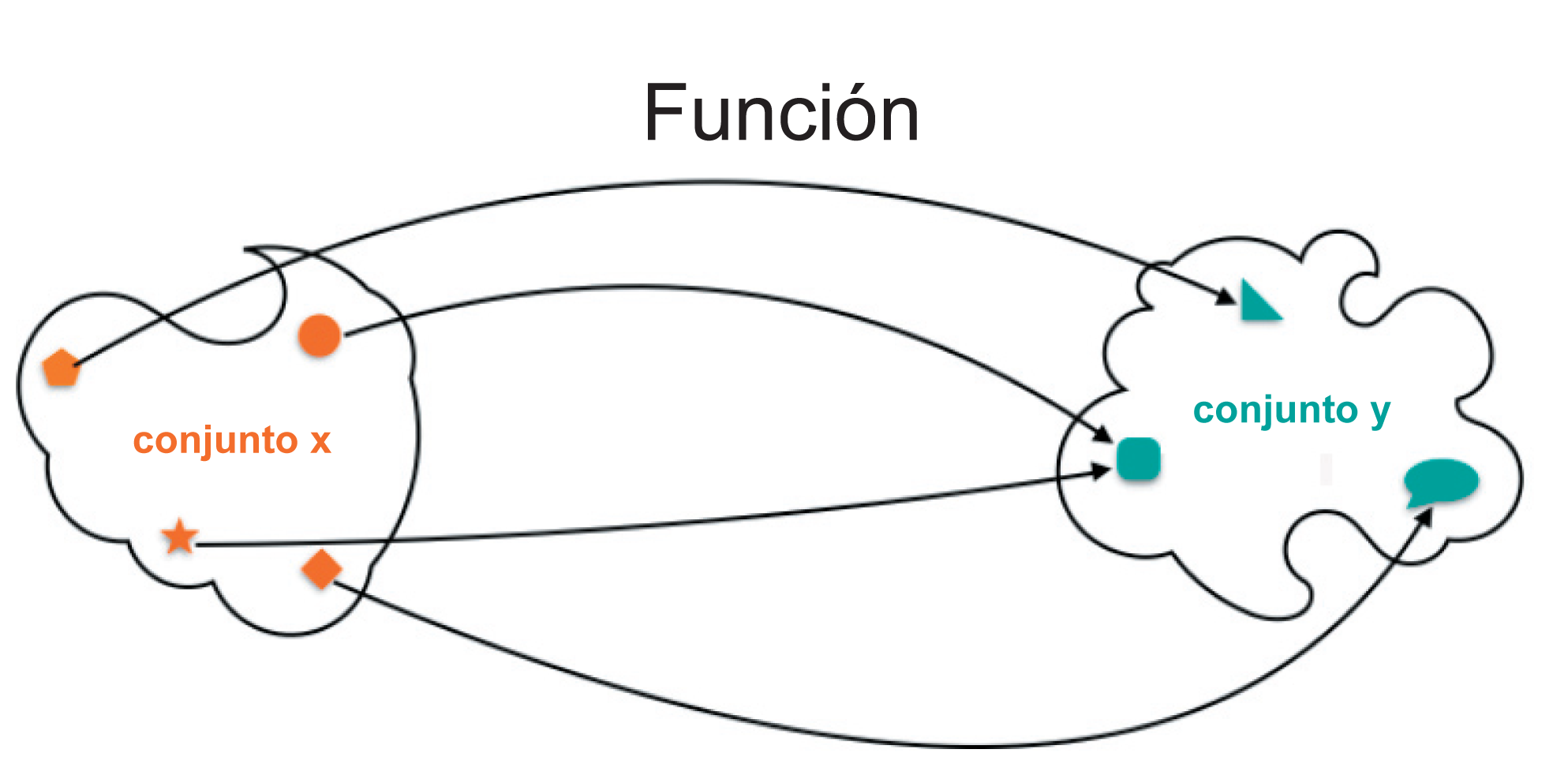
Una función es una asignación donde,
cada elemento de un conjunto (también llamado dominio)
evidentemente
asigna un elemento a un conjunto (también llamado contradominio).
El elemento es la variable dependiente, porque sus valores dependen del valor que le demos a la variable .
Nota: A menudo las funciones se designan con una sola letra. El nombre más común para una función es .
Con este nombre se puede aclarar fácilmente que es el valor de la función en la posición escribiendo . Esto se lee como " es igual a de ".
Ejemplos de Funciones
Ejemplo 1
será la función que asigne a cada animal el número de patas que este tiene normalmente. ¿Por qué es una función?
Simplemente:
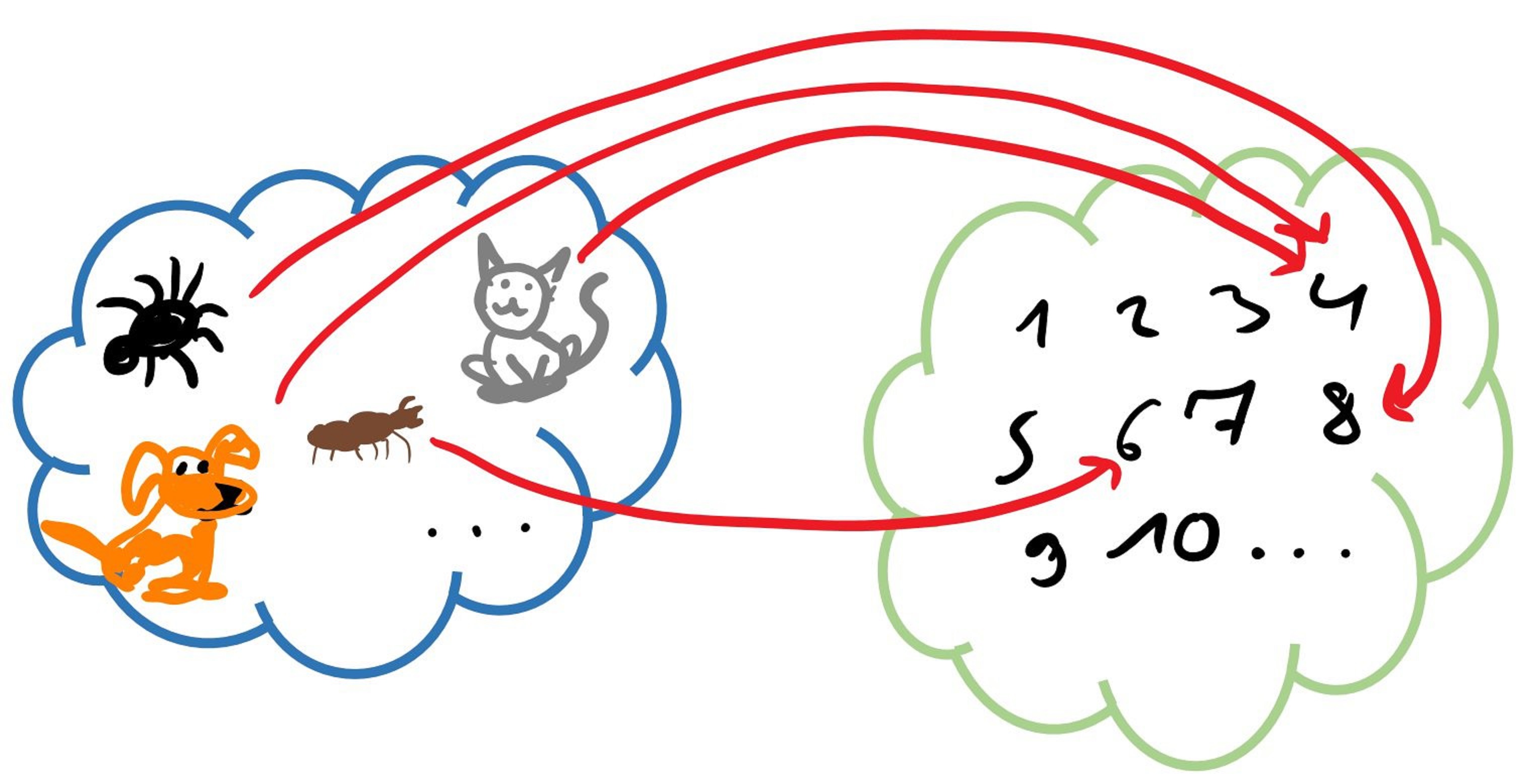
En este ejemplos los valores de las funciones pueden ser:
(gato) = ("el valor de la función en la posición del gato ")
(araña) = (" en la posición de la araña es 8")
(hormiga) = 6 (" en la posición de la hormiga es 6")
(perro) = 4 (" en la posición del perro es 5")
¿Por qué es una función?
Muy simple:
tiene un rango de definición (el conjunto de todos los animales).
tiene un rango de valores (el conjunto de todos los números naturales con el cero)
y el número de patas puede ser evidentemente asignado a cada animal.
Ejemplo 2
Pensemos por ejemplo en una persona que utiliza su celular para hacer una llamda, y por el tiempo conversado recibe una cuenta por un valor a pagar.
Decimos entonces, que el costo de la llamada es una función del número de minutos . Su notación matemática es:
o también
" es igual a una función de "
Decimos que es la variable arbitraria o independiente, pues la duración de la llamada depende del capricho o las ganas de hablar de la persona.

Imagen 1.
Una función es una relación entre dos conjuntos, es decir, un subconjunto del producto cartesiano , que cumple con las propiedades descritas arriba.
Supongamos que la persona tienen un contrato de celular que le cobra por cada minuto hablado.
Así pues el costo de la llamada vendría dado entonces por la expresión:
En cambio el costo de la llamada variará con el número de minutos conversados. Y depende de la cantidad de minutos. Así pues es la variante dependiente.
En este ejemplo, el rango de definición viene dado por los números naturales incluyendo el cero (). Según la definición del ejercicio, los minutos se redondean hacia arriba o hacia abajo.
El gráfico muestra evidentemente que cuanto más tiempo llames, más aumentan los costos.
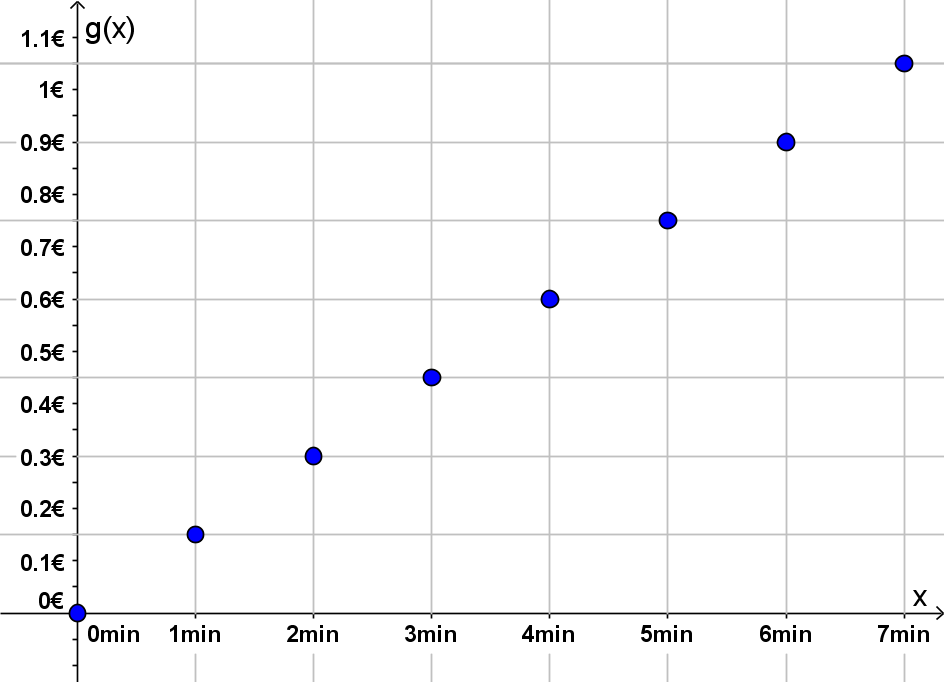
Ejemplo 3
será la función que asigna el doble del valor de cada número natural.
Para cada número, esta asignación es evidente.
Ejemplos de valores de función:
(el doble de es 2
Otros tipos comunes de notación
Se utiliza un ejemplo para comparar las designaciones de uso frecuente.
Al principio está la regla de asignación, que define el nombre, la variable y el valor de la función:
Dado que los valores de la función se calculan muy a menudo con una fórmula, es decir, un término, este término suele especificarse en lugar de
Por ejemplo:
Así que esta función se llama . Con la función se asigna un valor a cada valor que se le da a , el cual se calcula utilizando el término de la función . Los valores que se le dan a se seleccionan de la definición que tiene el conjunto de X, también llamado dominio y se denota por . Otros nombres comunes además de la son o con índice, por ejemplo o .
Lo importante es poder identificar el término de la función. Para cada término, las variables de término se dan entre paréntesis. En la mayoría de los casos sólo aparece la variable . Así, el término de la función se denomina o ) o , dependiendo del nombre que se le haya dado a la función.
Para el ejemplo de arriba se escribe:
Sobre la igualdad de la función: Hasta ahora, deciamos que a la según el término funcional , se le asigna una claramente definida. Si se consideran estos valores como pares de valores , entonces la puede ser calculada a partir de la con una ecuación:
Así que hay una ecuación con dos variables.
Por lo tanto, la igualdad entre dos expresions algebraicas puede considerar la regla de asignacion para resolver la ecuación.
Esto es importante cuando se introducen funciones en un sistema x-y de coordenadas a través de valores . Este conjunto de puntos formado por los pares de valores se llama la gráfica de la función , se denota . La gráfica es el conjunto de todos los puntos:
Importante: A menudo se utilizan otras letras para los nombres de las funciones y las variables. En la física, por ejemplo, t se utiliza como variable si es para describir el tiempo.
Si trabajas con varias funciones al mismo tiempo, puedes nombrar una como , otra como , otra como y así sucesivamente.
Algunos conceptos más avanzados
Las funciones también pueden tener propiedades especiales como:
Continuidad
Una función es continua cuando los valores pares en su gráfica se pueden trazar sin levantar la punta del lápiz al dibujarla, es decir no tiene interrupciones.
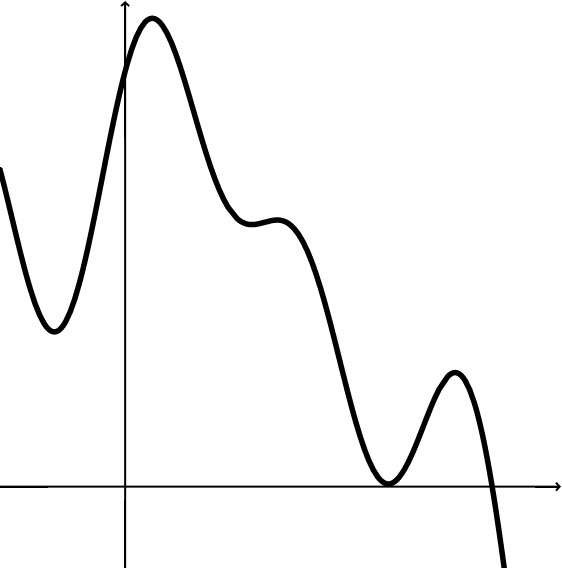
Diferenciable
La diferenciación de una función significa que el gráfico de la función tiene una tangente claramente definible en cada posición.

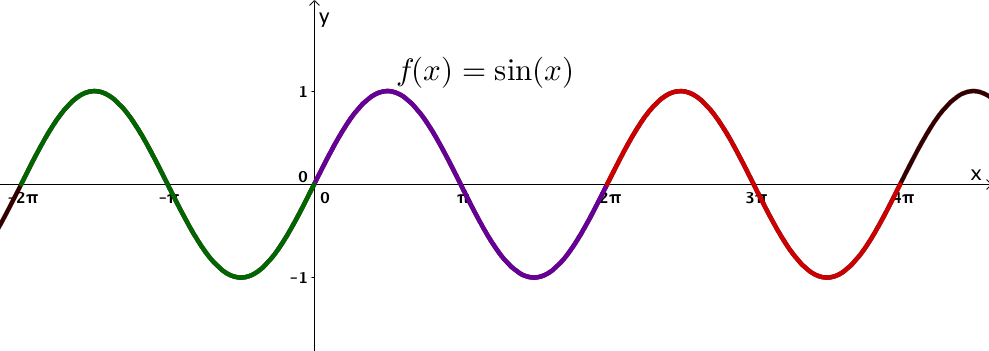
Periodo de la función
En algunas funciones, los valores de la función se repiten en intervalos regulares. Si este es el caso, la longitud del segmento más corto se denomina período de la función.
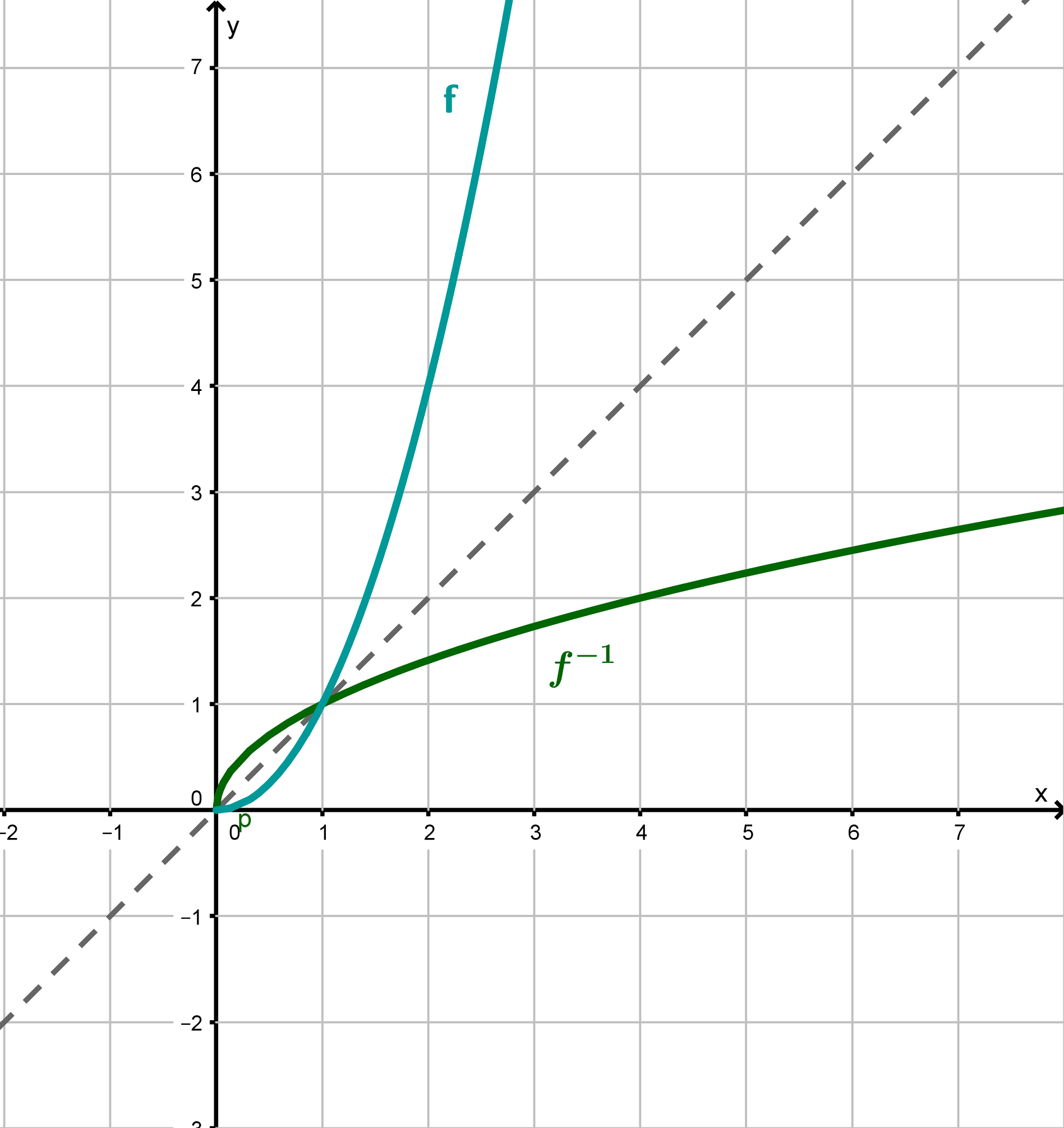
Función inversa
La función inversa de una función es la función , que asigna a cada valor de función su atributo:
Fuentes:
Imagen 1: : pxhere.com, Creative Commons CC0