Área de las figuras compuestas

Conocimientos básicos: Área de las figuras simples

El área de un rectángulo se calcula multiplicando la longitud por el ancho:

$A_{rectánculo}=\textcolor{006400}{Largo}\cdot \textcolor{009999}{Ancho} = \textcolor{006400}{l} \cdot \textcolor{009999}{a}$

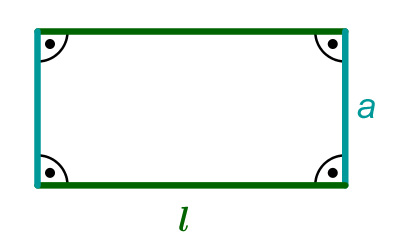
El área de un triángulo se calcula multiplicando la base $\textcolor{006400}{g}$ por la altura $\textcolor{009999}{h}$ y dividiendo por 2: $A_{\bigtriangleup }=\frac{1}{2} \cdot \textcolor{006400}{g}\cdot \textcolor{009999}{h}$

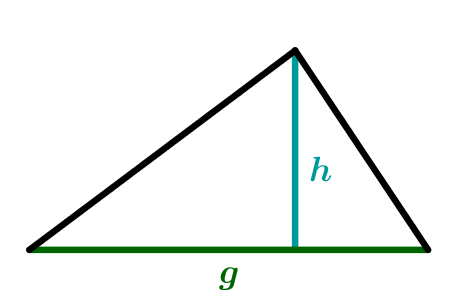
Descomposición en rectángulos y triángulos

Las figuras más difíciles a veces pueden dividirse en varios rectángulos y/o triángulos. Con este truco también puedes calcular fácilmente su área.

Ejemplo

Para determinar el área de esta figura, puedes proceder así:

Primero piensa en qué formas geométricas conocidas puedes descomponer la figura.
Ahora calcula el área de las formas conocidas con la ayuda de las fórmulas respectivas.
Obtendrás el área total de la figura añadiendo la suma de las áreas calculadas.

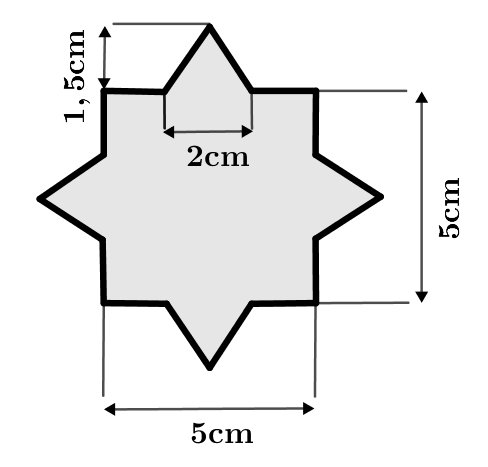
1. Determinación de las cifras conocidas:

Por ejemplo, la figura puede descomponerse en $\textcolor{ff6600}{un\,\,\,\ rectángulo}$ y $\textcolor{660099}{cuatro \,\,\, triángulos\,\,\,\, iguales}$ .

Nota: Aquí se trata incluso de un rectángulo especial, ¡un cuadrado!

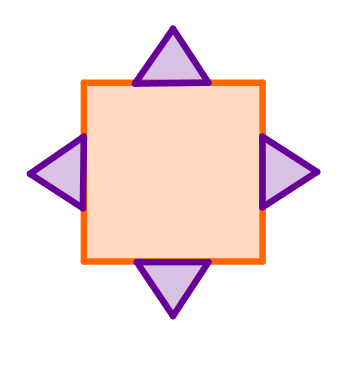
2. Calcular el área de las figuras conocidas:

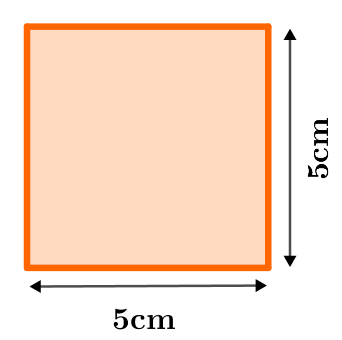
$\textcolor{ff6600}{Rectángulo:}$ El área del rectángulo puede calcularse utilizando las fórmulas anteriores e insertando los valores adecuados.

$A_{Rectánculo}\,\, = \text{l} \cdot \text{a}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5\,\,\text{cm}\cdot5\,\,\text{cm}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=25\,\,\text{cm}^2$

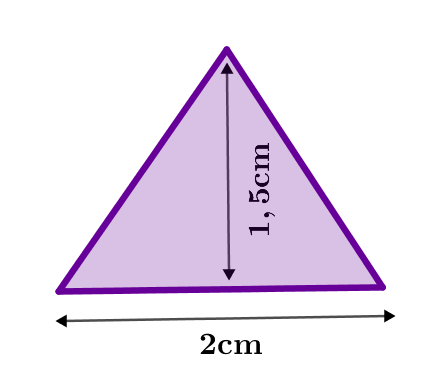
$\textcolor{660099}{Triángulo:}$ El área del triángulo se puede calcular utilizando la fórmula indicada anteriormente e insertando los valores correspondientes.

$A_{Triángulo}\,\, = \frac{1}{2} \cdot {g}\cdot {h}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}\cdot 2\,\,\text{cm}\cdot1{,}5\,\,\text{cm}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=1{,}5\,\,\text{cm}^2$

3. Área de la figura completa:

La suma de las áreas individuales proporciona el área de toda la figura.

Vorsicht

hay que tener en cuenta que la figura tiene $\textcolor{cc0000}{{cuatro}}$ triángulos.

$A_{\,\,Figura \,\, completa}\,\, = A_{Rectánculo} + \textcolor{cc0000}{4}\cdot A_{Triángulo}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=25\text{cm}^2+ \textcolor{cc0000}{4}\cdot1{,}5\,\,\text{cm}^2\\\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=25\,\,\text{cm}^2+6\,\,\text{cm}^2\\ \,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=31\,\,\text{cm}^2$

Por tanto, el área de la figura es $31\,\,\text{cm}^2$ .

Agregando un rectángulo

A veces el área de las figuras difíciles puede calcularse agregando primero la figura a una forma conocida y restando después las formas que no pertenecen a la figura.

Ejemplo

Para determinar el área de esta figura (un octágono), puedes proceder como sigue, por ejemplo:

Piensa primero en qué forma geométrica conocida puedes añadir a la figura.
Ahora calcula el área de la forma conocida utilizando la fórmula correspondiente.
Determina las formas geométricas que no pertenecen a la figura y réstalas de la forma completa para obtener sólo el área de la figura.

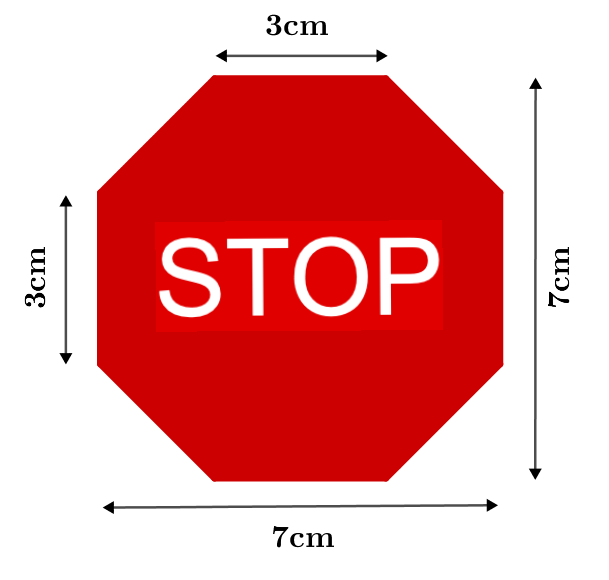
1. Adición a una figura conocida:

Por ejemplo, la figura puede completarse con $\textcolor{009999}{un \,\, rectángulo}$ .

Beachte

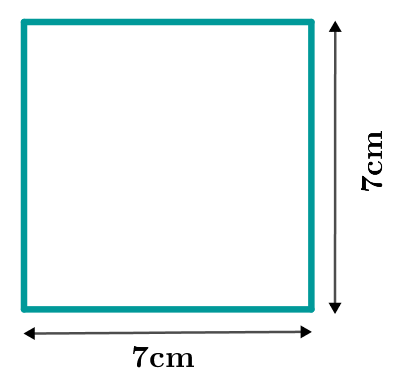
Aquí se trata incluso de un rectángulo especial, ¡un cuadrado!

2. Calcula el área de la figura conocida:

$\textcolor{009999}{Rectángulo}$ : El área del rectángulo se puede calcular utilizando las fórmulas indicadas anteriormente e insertando los valores correspondientes.

$A_{Rectánculo}\,\, = \text{l} \cdot \text{a}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=7\,\,\text{cm}\cdot7\,\,\text{cm}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=49\,\,\text{cm}^2$

3. Resta las formas que no pertenecen a la figura:

Para obtener el área de la figura, todavía tenemos que restar los $\textcolor{660099}{cuatro\,\,\,\,triángulos\,\,iguales.}$

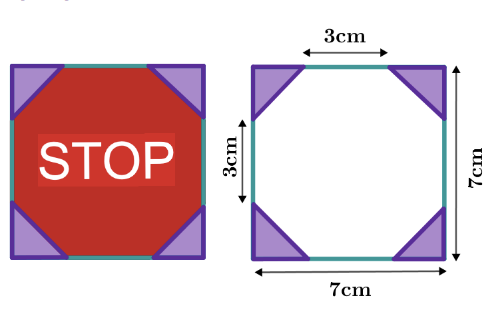
El área del triángulo se puede calcular con la ayuda de la fórmula indicada anteriormente e insertando los valores correspondientes. Para ello necesitas el lado de la base $g$ y la altura $h$ del triángulo.

Determinación del lado: La longitud del lado del rectángulo es de $7 \text{cm}$ y la del octágono es de $3 \text{cm}$ . Restando la longitud de los lados del octágono a la longitud de los lados del rectángulo se obtienen los lados de dos triángulos.

\displaystyle 7 \text{cm}-3 \text{cm}=4 \text{cm}

Como son dos triángulos iguales, puedes determinar el lado de uno de los triángulos dividiendo el $4 \text{cm}$ entre $2$ .

\displaystyle 4\text{cm}:2=2\text{cm}

Por lo tanto, el lado de la base del triángulo mide $2 \text{cm}$ . Como el rectángulo es un cuadrado, todos los lados tienen la misma longitud y, por tanto, todos los lados de los triángulos que se encuentran en el lado del cuadrado miden $2 \text{cm}$ .

Determinación de la altura: Si observas los triángulos más de cerca, puedes ver que son triángulos rectángulos. Esto significa que la altura también es de $2 \text{cm}$ .

Área del triángulo:

$A_{Triángulo}\,\, = \frac{1}{2} \cdot {g}\cdot {h}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}\cdot 2\,\,\text{cm}\cdot2\,\,\text{cm}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\,\,\text{cm}^2$

Área de toda la figura:

Restando los triángulos del rectángulo obtenemos el área de toda la figura.

Vorsicht

Hay que tener en cuenta que hay que restar $\textcolor{cc0000}{cuatro}$ triángulos.

$A_{\,\,Figura \,\, completa}\,\, = A_{Rectánculo} - \textcolor{cc0000}{4}\cdot A_{Triángulo}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=49\text{cm}^2- \textcolor{cc0000}{4}\cdot2\,\,\text{cm}^2\\\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=49\,\,\text{cm}^2-8\,\,\text{cm}^2\\ \,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=41\,\,\text{cm}^2$

Conocimientos básicos: Área de las figuras simples

Descomposición en rectángulos y triángulos

Agregando un rectángulo

Du hast noch nicht genug vom Thema?

Artikel