Redondear números naturales

Al redondear un número, en lugar del valor exacto del número, se especifica un número cercano al número pero "redondeado" (en el sentido coloquial), por ejemplo, un número en decenas, centenas, miles.

El objetivo principal del redondeo es simplificar un número; porque a veces simplemente no es necesario o posible ser completamente preciso con un número.

Cuando redondeas un número, lo anotas con un $\approx$ ("aproximadamente") entre los números.

• Al redondear números, debes tener en cuenta a qué lugar quieres redondear el número.

• Se distingue entre el redondeo de números decimales y el redondeo a lugares específicos.

• También se explica el término "redondeo sensible".

Procedimiento

Caso especial: El número ya es esta "redondeado"

En este caso, no hay nada que hacer: El número simplemente sigue siendo el número que se tiene.

Ejemplo:

• El número $700$ es $700$ redondeado a la centena más cercana.

Caso normal: El número no está "redondeado".

En este caso, consideramos dos números "redondeados" que se acercan al número:

• uno por debajo y otro por encima.

• de estos dos, ahora eliges el que está más cerca del número.

Cuando redondeas y elijes el menor de los dos números, se llama redondear hacia abajo; si es el mayor, se llama redondear hacia arriba.

La convención: En matemáticas, si el número dado está exactamente a mitad de camino entre los dos números "redondeados", se suele redondear hacia arriba y no hacia abajo.

1- Ejemplo:

Redondea las centenas del número $2734$ . Los dos números de centenas entre los que se encuentra son:

• $2700$ (es menor que $2734$)

• $2800$ (es mayor que $2734$)

Como $2734$ está más cerca de $2700$ que de $2800$, el número se redondea a $2700$.

2- Ejemplo:

Redondea las decenas del número $385$ . Los dos números de la decena entre los que se encuentra son:

• $380$ (es menor que $385$)

• $390$ (es mayor que $385$)

Como el $385$ está exactamente a mitad de camino entre el $380$ y el $390$, es equidistante de ambos. Normalmente, en matemáticas, se redondea hacia arriba en un caso así. Es decir, $385$ redondeado a decenas da $390$.

Consejo para el procedimiento práctico

Es importante:

Redondeo a lugares específicos

Puedes redondear no sólo a números enteros, es decir, al lugar de las unidades, sino a cualquier lugar del número. Redondear a dígitos concretos significa que buscas el número decimal que termina con el dígito al que quieres redondear.

Tabla de valor posicional:

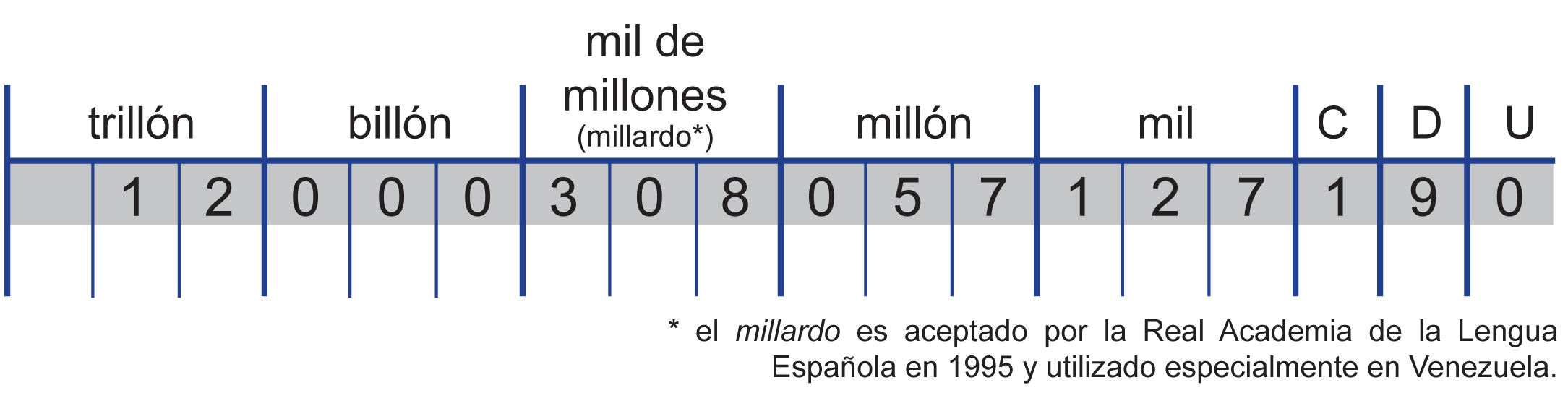
Para decidir si redondear hacia arriba o hacia abajo (=mantener) el dígito, aquí sólo se mira el dígito que está directamente a la derecha del dígito que buscas.

La regla también se aplica aquí:

• Redondea hacia abajo, si el dígito considerado está entre 0 y 4,

• Redondea hacia arriba, si el dígito considerado está entre 5 y 9.