Introducción a las fracciones

Curso

1 Descripción general

Contenido del curso

El objetivo del curso es conocer el concepto de fracciones.

Mediante representaciones gráficas, aprenderás qué son las fracciones, qué son las fracciones mixtas, cómo se pueden representar las fracciones en la recta numérica y qué características especiales tienen las fracciones.

Duración del curso

El curso dura aproximadamente 1 hora

2 ¿Qué es una fracción?

Juana celebra una fiesta de cumpleaños con sus 3 mejores amigas Catalina, Lisa y María. Ellas cortaron el pastel en 12 trozos.

Juana se come 3 pedazos.

Esta proporción se escribe como $\frac{3}{12}$ , porque son tres doceavos del pastel.

Catalina sólo se come un trozo del pastel, $\frac{1}{12}$ . Lista también come un trozo, $\frac{1}{12}$ . María come $\frac{2}{12}$ .

$1$ doceavo, $\frac{1}{12}$ .

$2$ doceavos, $\frac{2}{12}$ .

Quedan $5$ trozos, así que de escribe $\frac{5}{12}$ .

Una sección de este tipo se llama fracción. Una fracción (por ejemplo $\frac{5}{12}, \frac{3}{5}, \frac{7}{190}$ ) consiste en dos números (numerador y denominador) separados por una barra de fracción.

El numerador (arriba) indica el número de trozos:

Junana come $3$ doceavos. Numerador: $3$
Quedan $5$ doceavos. Numerdor: $5$

El denominador (abajo) indica el tipo de trozos:

El "doceavo" quiere decir que el pastel se partió en $12$ pedazos iguales. Denominador: $12$

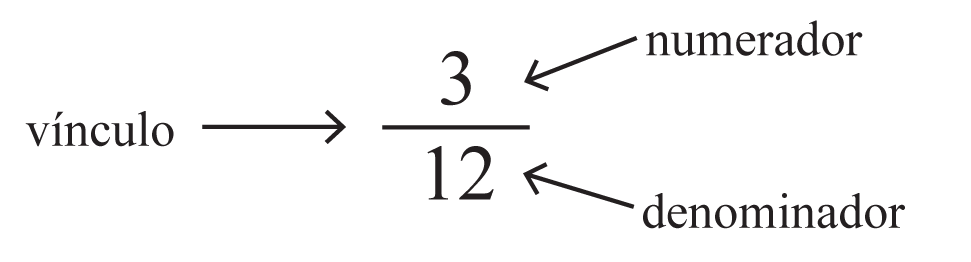
3 Representación de fracciones

Del mismo modo, con las fracciones puedes describir partes de otras cosas, por ejemplo, partes de círculos o rectángulos.

Ejemplos

El círculo se divide en $6$ partes iguales ("sextos"). Así que el denominador es $6$ .

De todos los sextos, $2$ sextos son de color, por lo que el numerador es $2$ .

Así que esta imagen representa la fracción $\frac{2}{6}$ .

El rectángulo se divide en $4$ partes iguales ("cuartos"). Así que el denominador es $4$ .

De los cuartos, $1$ es de color, por lo que el numerador es $1$ .

Así que esta imagen representa la fracción $\frac{1}{4}$ .

En general

La fracción se determina como $\frac{p a r t e}{t o d o}$ .

Cuenta cuántas piezas del mismo tamaño hay en total (sean de color o no). Este es el denominador.
Cuenta cuántas piezas son de color. Este es el numerador.

ATENCIÓN: Las partes deben ser todas del mismo tamaño. De lo contrario, córtalas, o pon varias juntas, para que las piezas sean todas del mismo tamaño al final.

4 Ejercicios

Laden

5 Fracciones en la recta numérica

También puedes dibujar fracciones en la recta numérica. Para ello, divide la recta numérica entre el 0 y el 1 en partes iguales. Por ejemplo, en $3$ partes ("tercios"):

Arriba se ha dibujado la fracción $\frac{1}{3}$ en la recta numérica. Ahora se puede hacer lo mismo con el $\frac{2}{3}$ :

Si dibujas el $\frac{3}{3}$ , estarás en el $1$ .

$\frac{0}{3}$ también pueden ser dibujadas:

Las fracciones pueden dibujarse en la recta numérica dividiendo la recta numérica entre el 0 y el 1 en partes iguales.

6 Vídeo: Fracciones en la recta numérica

Laden

7 Ejercicios

Laden

8 Fracción como división

A menudo también es útil otra idea sobre las fracciones: las fracciones son otra forma de escribir la división.

Ejemplo

\frac{3}{5} = 3 : 5

Para representar $\frac{3}{5}$ como una fracción, divide un entero en $5$ partes y pinta $3$ de ellas.

Para representar la división $3 : 5$ , divides $3$ enteros en $5$ partes.

La parte roja es la misma en ambas representaciones. Así que también $\frac{3}{5} = 3 : 5$

También puedes escribir la fracción $\frac{n}{d}$ como la división $n : d$ .

Así que la línea de fracción significa "dividido".

9 ¿Qué es una fracción mixta?

Las fracciones mayores que 1 suelen representarse como fracciones mixtas.

Ejemplo

3 \frac{7}{12}

Esta notación significa: tienes $3$ enteros y $\frac{7}{12}$ de otro entero. Es una forma abreviada de $3 + \frac{7}{12}$ .

Una fracción mixta está formada por un número entero y una fracción.

10 Ejercicios

Laden

11 Convertir una fracción mixta

También puedes convertir un número mixto en una fracción normal.

2 \frac{1}{3}

En la imagen de arriba puedes ver que los 2 enteros se pueden dividir en 6 tercios. Junto con el $\frac{1}{3}$ hay $\frac{6 + 1}{3} = \frac{7}{3}$ .

Una fracción de este tipo también se llama fracción impropia. El numerador es entonces mayor que el denominador.

Procedimiento

Primero, calcula en cuántas partes se dividirá el entero. Multiplica el entero por el denominador.
Luego suma este número y el numerador de la fracción. Este es el nuevo numerador de la fracción impropia.

¡El denominador no cambia!

Ejemplo

$3 \frac{2}{5}$

Los 3 enteros se dividen en $3 \cdot 5 = 15$ partes.

Por lo tanto, en total hay $\frac{15 + 2}{5} = \frac{17}{5}$ .

Este contenido está licenciado bajo
CC BY-SA 4.0 → Información