Números Primos

Los números primos se utilizan para codificar y encriptar los mensajes y datos.

Ejemplos:

• El $22$ sí es un número primo, además es el único número primo que es par.

• El $55$ sí es un número primo, porque es mayor que $22$ y no tiene otros divisores aparte de si mismo y $11$.

• El $66$ no es un número primo, porque $11$ y $66$ son sus divisores, además del $22$ y $3.3.$

• El $2727$ no es un número primo, porque tiene más de dos divisores: $11$, $33$, $99$ y $2727$.

• El $4141$ sí es un número primo, porque es mayor que $22$ y no tiene otros divisores aparte de sí mismo y $11$.

• El $6363$ no es un número primo, porque tiene más de dos divisores: $11$, $77$, $99$ y $6363$.

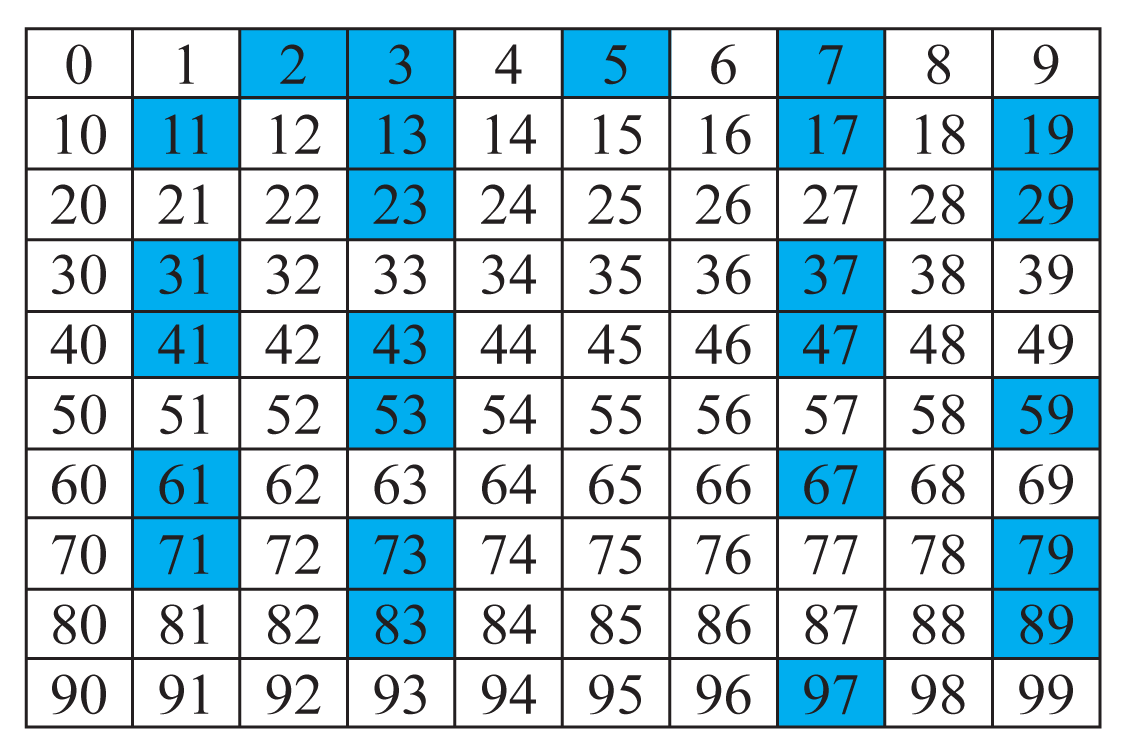
Los números primos de 0 a 99

Los siguientes números entre 0 y 99, resaltados en cuadrado azul, son números primos:

Método para comprobar si un número es primo

Si tienes un número y necesitas comprobar si él es un número primo, el método más fácil es intentar dividirlo por todos los números primos hasta que puedes identificar su conjunto único de factores primos.

Entonces compruebas si el número es divisible por $22$, luego por $33$, luego por $5_{}5\_\{\; \}$, y así sucesivamente...

Si se han excluido hasta su raíz todos los números primos hasta el número dado, entonces el número en sí es un número primo. De lo contrario, no lo es.

Por supuesto, hoy en día se utilizan otros métodos con los computadores.

Ejemplo:

Tomemos el número 25.

• El $2525$ se puede dividir por $11$. $25:1=2525:1=25$

• El $2525$ no se puede dividir por $22$. $25:2=12.525:2=12.5$

• El $2525$ no se puede dividir por $33$. $25:3=8.33325:3=8.333$

• El $2525$ se puede dividir por $55$ $25:5=525:5=5$

• El 25 se puede dividir por 25 $25:25=125:25=1\backslash \backslash$ el conjunto de factores primos para $2525$ tiene 3 factores $\Rightarrow \backslash \backslash \; \backslash Rightarrow$$25(1,5,25)25(1\{,\}5,25)$ El 25 no es un número primo

Por supuesto, las computadoras de hoy en día también utilizan otros métodos, especialmente cuando queremos saber si un números grande es primo.

Descomposición en factores primos

Como lo muestra el ejemplo anterior, cuando comprobamos si un número es primo, en el proceso descomponemos el número en un conjunto de factores primos. Un factor primo es aquel número primo $\mathcal{p}\backslash mathcal\{p\}$ que divide a cualquier número $nn$.

Descomponer en factores primos es posible para un número $nn$, teniendo en cuenta que $nn$ no es un número primo y además es mayor a 2. El resultado es un conjunto unico de números primos.

Tomemos como $nn$ al número $4848$, que no es un número primo porque a simple vista tiene más de dos divisores: el $22$ además de $11$ y $4848$. Podemos escribir:

El número $22$ es un número primo y por lo tanto no puede ser descompuesto en un conjunto de factores menores a $22$. Por el contrario, $2424$ no es un número primo y puede descomponerse aún más (por ejemplo, $44$ es un divisor de $24)24)$. Así que $2424$ puede descomponerse aún más:

Mientras no tengamos números primos en los factores, podemos seguir descomponiéndolo aún más hasta que sólo tengamos un conjunto de números primos como factores:

Así pues, si un número natural mayor o igual a $22$ se descompone cada vez más en factores, en algún momento se obtiene un conjunto único de factores que contiene sólo números primos. La descomposición de un número en un conjunto de factores que son números primos se llama método para descomponer en factores primos.

Ejemplo

Realizemos la descomposición en factores primos para el $2121$:

$21=3\cdot 721=3\backslash cdot7$

Infinidad de números primos

La cantidad de números primos es infinita. Así que no puedes encontrar el mayor número primo. Siempre habrá un número primo que sea mayor. La prueba de esta tesis fue dada por Euclides hace más de 2000 años.