Segmento
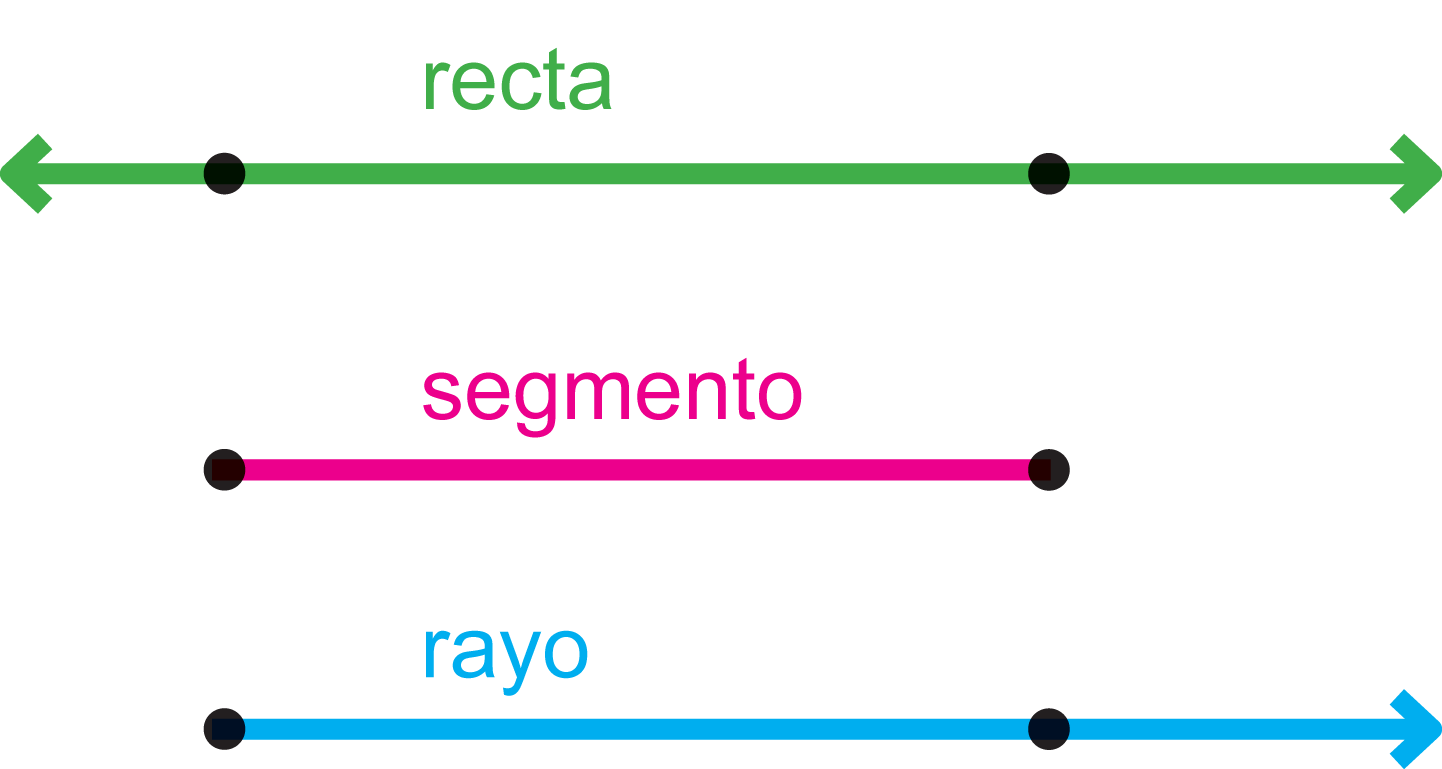
Relación entre la recta y el segmento
Si consideramos una recta g y los dos puntos A y B que se encuentran sobre ella, la distancia [AB] es el segmento que se encuentra entre los dos puntos. Por lo tanto, un segmento está limitado por sus dos puntos extremos, a diferencia de la recta que continúa infinitamente en ambas direcciones.
Punto medio de un segmento
El punto medio de una recta [AB] es el punto en [AB] donde la distancia a A y B es exactamente igual.
En la gráfica este está marcado como

Dibujar el punto medio en un segmento
Para construir el punto medio de una recta, sólo hay que dibujar su perpendicular.
Dadas las coordenadas del punto inicial y del punto final de una recta, se puede calcular el punto medio de la siguiente manera:
Distancia
La longitud de un segmento se denota por . es la distancia entre los puntos y .
Distancia euclidiana
Si estás en el sistema de coordenadas cartesianas, la distancia se calcula mediante el teorema de Pitágoras.
Loading
Esto funciona figurativamente de la siguiente manera:
El componente del punto se resta del componente del punto , esto también se hace con los componentes . Los dos valores resultantes son las longitudes de los catetos de un triángulo rectángulo, el lado que falta es la distancia buscada de los puntos, que ahora se puede calcular muy fácilmente utilizando el teorema de Pitágoras.
Still want more?
You can find more content on this topic here: