Ley distributiva
La Ley distributiva nos indica cómo resolver expresiones matemáticas de multiplicación o división que tienen paréntesis.
Es especialmente útil cuando las variables dentro del paréntesis no son numéricas, es decir que tienen letras. Como esta:
así mismo
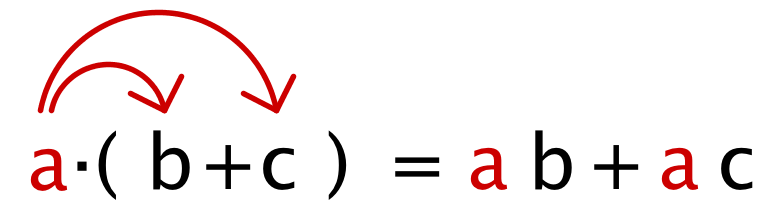
La ley distributiva para cálculos numéricos
Ventaja de calcular con la ayuda de la ley distributiva
La ley de distribución puede utilizarse para simplificar algunas tareas de cálculo:
En ejercicios de multiplicación, a veces uno de los dos factores puede descomponerse de manera que la ley distributiva da lugar a dos multiplicaciones, cada una de las cuales es más sencilla que la multiplicación original. otro ejemplo:
A veces se puede ahorrar trabajo multiplicando varios números por el mismo valor y sumando o restando los resultados aplicando la ley distributiva al contrario.
Aplicación en de la ley distributiva en la división
Debemos tener encuenta que en el caso de una división, la ley de distribución puede aplicarse a los dividendos, pero no al divisor:
Ejemplo con los dividendos:
es lo mismo que
entonces,
Ejemplo con el divisor:
pero,
y son respuestas muy diferentes. Por esta razón esta ley distributiva no aplica al divisor.
La ley distributiva para cálculos con variables
Multiplicando el contenidode los paréntesis
Signo negativo antes de los paréntesis
Un caso especial de la ley distributiva es cunado hay un menos antes de un paréntesis.
Ejemplo:
También podemos escribir el menos como , así:
Ahora ponemos el (-1) en el paréntesis:
Si se multiplican los términos, sólo cambia el signo respectivo:
Si ahora eliminamos el (-1), hemos alcanzado de nuevo nuestro punto de partida.
Colocar paréntesis a un factor
(es simplemente al contrario, como en la multiplicación)
Ejemplos:
Buscamos el factor común :
Colocamos un paréntesis:
Multiplicación o división
Si hay una multiplicación o división entre paréntesis, no se aplica la ley distributiva. Para saber cómo se pueden deshacer los paréntesis en este caso, puedes leer el artículo Multiplicando el contenido de los paréntesis.
Still want more?
You can find more content on this topic here: