El máximo dominio de la función (conjunto de definición) de una ecuación fraccionaria indica qué valores pueden utilizarse para la variable.
Los dos denominadores no deben ser cero.
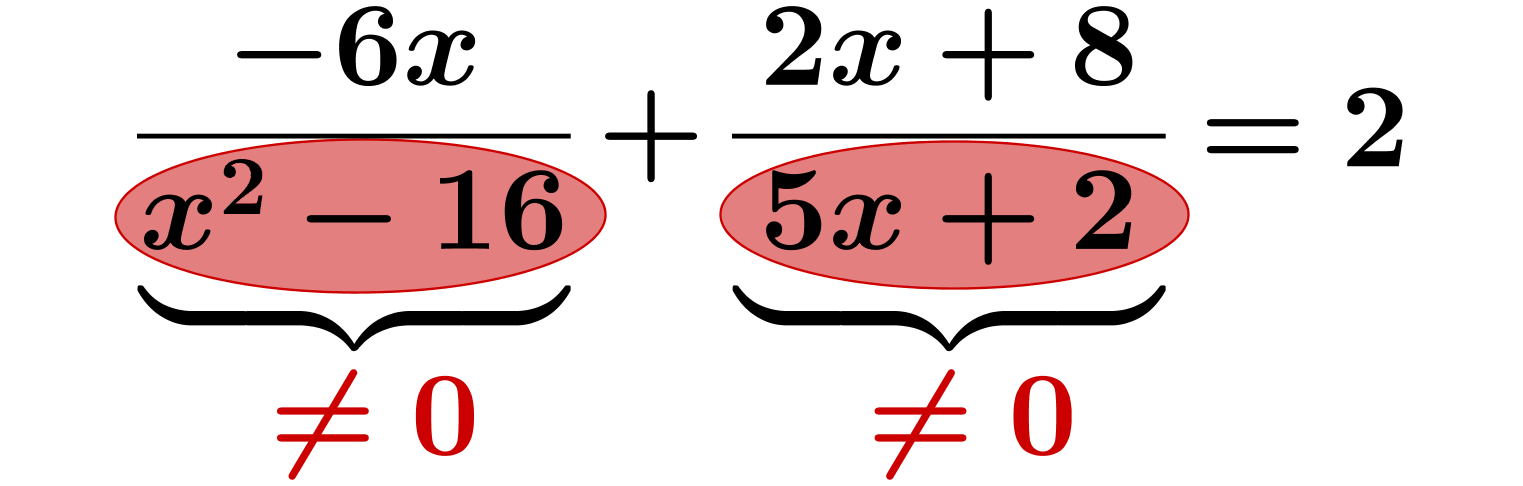
El denominador no debe ser 0
Nunca debe haber un cero en el denominador de una fracción. Por tanto, todos los números para los que el cero resulta en algún lugar del denominador cuando se insertan en la ecuación deben excluirse del dominio (conjunto de definición) de una ecuación fraccionaria.
Notación matemática
Para excluir números del dominio, utiliza el carácter de operación de conjunto (es decir, un trazo inclinado hacia atrás).
"" significa "sin".
Después vienen los números excluidos.
Alrededor de estos números hay un corchete: "{...}".
Nota sobre el dominio
Por regla general, se utiliza como dominio de la función (conjunto de definición) el mayor conjunto posible de números disponibles.
Dependiendo del grado escolar y del plan de estudios, puede ser el conjunto de los números reales o sólo el conjunto de los números racionales.
Procedimiento para determinar el domino
Para cada una de las fracciones que se producen escribe el denominador
ponlo a
y resuelve la variable.
Todos los números que se obtengan como soluciones deben ser excluidos del conjunto de definiciones:
Escribe el conjunto básico (normalmente o ),
luego escribes
y luego entre corchetes todos los números para los que cualquier denominador sería cero.
Procedimiento general explicado con el ejemplo
Ejemplo:
Para cada una de las fracciones que se producen escribe el denominador: y
ponlo a y
y resuelve la variable. y
Todos los números que se obtengan como soluciones deben ser excluidos del conjunto de definiciones:
Escribe el conjunto básico (normalmente o )
luego escribes
y luego entre corchetes todos los números para los que cualquier denominador sería cero. En el ejemplo obtienes: si el conjunto de definición es , por ejemplo, , si el conjunto de definición es .
¿Por qué es importante la definición máxima establecida?
Por regla general, antes de resolver la ecuación fraccionaria, se determina el rango del dominio (o el conjunto de definición) de la ecuación fraccionaria.
Más tarde, cuando hayas resuelto la ecuación y obtenido un resultado, tienes que comprobar si está en el rango del dominio. Si no está en el rango del dominio, no es la solución de la ecuación, aunque hayas calculado correctamente.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
