El dominio de una función (también: el conjunto de definición o conjunto de partida) indica qué valores pueden insertarse en una función.
Descripción con ejemplos
Hay diferentes maneras de representar el dominio
"El dominio está formado por , , etc."
"El dominio son los valores desde hasta etc."
"El dominio son todos los números reales excepto ."
Vídeo sobre el dominio y el rango de una función
Laden
Brechas en la definición
Para determinar dominio una función, hay que comprobar si hay vacíos o brechas de definición.
Estos son valores que no pueden ser insertados en una función. Así que hay que comprobar si para un determinado valor
el denominador de una fracción sería ,
un número negativo estaría bajo una raíz,
el argumento de un logaritmo sería menor o igual a 0.
Identifica brechas de definición en el gráfico de la función
Una brecha de definición puede haber en:
Un punto o puntos de indefinición (que no toca o tocan la asíntota). Ejemplo son funciones con evidencia de comportmiento asintótico.
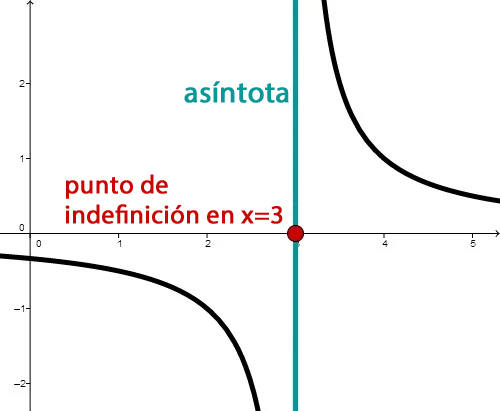
Una sección discontínua.

Una brecha o vacío en un punto. Ejemplo, función discontínua.

Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
