Ecuaciones lineales

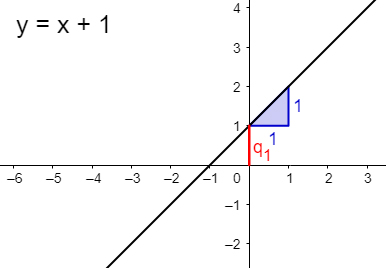
Fuente gráfica: En geogebra de Peter Mandak y Barbara Lichtenegger

Sin embargo, no es necesario elegir $x$ como variable, cualquier letra es posible:

• $3 \cdot A = 12$

• $3 \cdot b+5=12$

Las ecuaciones lineales con una variable pueden tener tres tipos de soluciones: ninguna, una o infinitas.

Ecuaciones lineales con más de una variable

También hay ecuaciones lineales con más de una variable:

• $3\cdot x + 2 \cdot y=7$

• $-x=2\cdot y$

Las soluciones de una ecuación lineal con dos variables también pueden tener ninguna, una o infinitas soluciones. Sin embargo, las soluciones en este caso son parejas.

$-x=2\cdot y$

Ecuaciones lineales con variables y parámetros

También hay ecuaciones lineales con una variable y parámetros. Los parámetros son números desconocidos que también se representan con una letra. Con este tipo de ecuaciones, hay que determinar o saber qué es la variable y qué es un parámetro:

• $a \cdot x = 4$ una variable x, un parámetro a

• $a\cdot x + b+\cdot y = c$ dos variables x e y; tres parámetros a, b y c

Transformaciones hasta encontrar la ecuación lineal

Muchas ecuaciones que no pueden identificarse inicialmente como ecuaciones lineales pueden reducirse a ecuaciones lineales mediante transformaciones:

• $x\cdot (x+4)=x^2+8$ el término cuadrático $x^2$ se elimina cuando se transforma

Resolver una ecuación lineal

Para resolver una ecuación lineal, se suele proceder como sigue:

1. Primero, resuelve todos los paréntesis.

2. A continuación, reformula la ecuación de manera que todos los términos con la variable queden a la izquierda y todos los que no tienen la variable (es decir, los números y los parámetros) queden a la derecha.

3. A continuación, se procede a reolver las expresiones aritméticas de ambos lados.

Puedes encontrar información más detallada sobre el procedimiento aquí: Transformaciones equivalentes