Función cero - el cero de una función

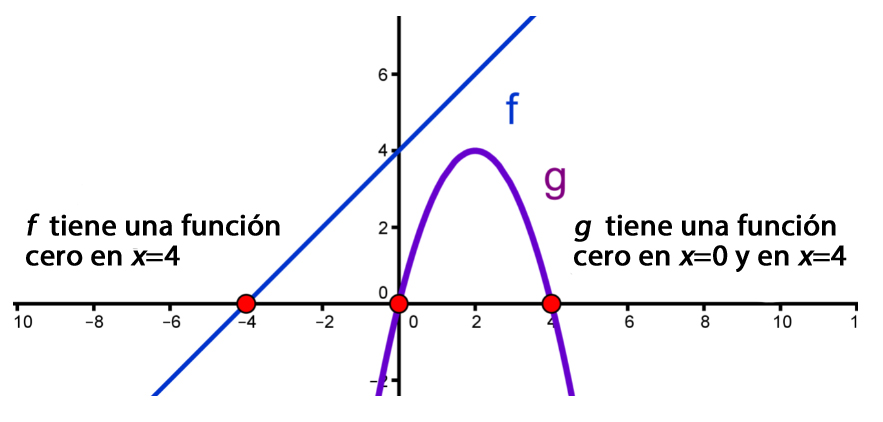
Ilustración en un applet

Calcular los ceros de una función

Raíz de multiplicidad en una función

En el caso de los polinomios, se distingue en función de sus multiplicidades. Esto indica la frecuencia con la que se produce un determinado cero en una función y viene determinada por los exponentes en la descomposición factorial lineal del polinomio.

La función $f$ con $f(x)=x^2-4$ tiene los ceros de la función $x=+2$ y $x=-2$. Su descomposición factorial lineal es por tanto $f(x)=(x-2)^{\color{red}{1}} \cdot(x+2)^{\color{red}{1}}$. Para ambos ceros de la función, el exponente respectivo del factor lineal es igual a $\color{red}{1}$. Así pues, los ceros de la función ocurren exactamente una vez en cada caso.

Estos tipos de ceros de la función se denominan raíz simple, o multiplicidad 1.

Múltiples raices de multiplicidad

Sin embargo, también hay funciones con los llamadas raices múltiples, donde hay varios ceros de la función.

La función $f$ con $f(x)=(x-2)^{\color{red}{2}} =(x-2)\cdot (x-2)$ tiene un doble cero de la función en $x=+2$.

Estos tipos de ceros de la función se denominan raices de multiplicidad 2.

La función $f$ con $f(x)=(x-2)^{\color{red}{3}} =(x-2)\cdot (x-2)\cdot (x-2)$ tiene un triple cero de la función en $x=+2$.

Estos tipos de ceros de la función se denominan raices de multiplicidad 3.

En consecuencia, hay funciones con cuatro, cinco, seis,... raices de multiplicidad.

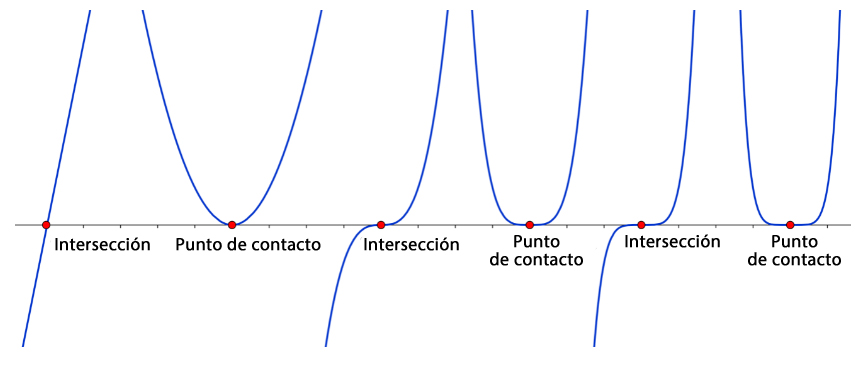
Significado gráfico de la multiplicidad

En un punto cero, la gráfica de una función $f$ interseca o toca el eje $x$. La existencia de una intersección o un punto de contacto puede determinarse por la multiplicidad de la raíz:

Así, se produce un cambio de signo en los puntos cero de la función con multiplicidad impar y no se produce ningún cambio de signo en los puntos cero de la función con multiplicidad par.

Representación gráfica: Puntos cero de la función con multiplicidad ascendente (1-6)

Ejemplos