Saltar a contenido o Pie de página
SerloLa Plataforma para el Aprendizaje Abierto

Calcular con unidades

En las tareas de aplicación de las matemáticas, a menudo se calcula no sólo con números, sino también con unidades, como kilogramos, litros, metros... Sin embargo, no hay que desanimarse por ello, ya que las unidades pueden tratarse como números en los cálculos.

Lo decisivo es pensar qué unidad debe salir y si entonces también tiene sentido. Al calcular áreas, por ejemplo, una unidad como m2\text{m}^2 tiene sentido, mientras que min2\text{min}^2 no tiene sentido.

VorsichtAntes de empezar ...

¡Es fundamental que te asegures de que las medias sean uniformes!

Sumar/restar unidades

Si sumas/restas unidades, los dígitos cambian, pero no las unidades. Siguen siendo las mismas. Para evitar confusiones al calcular, puedes pensar primero en la unidad, sumar/restar los dígitos y luego volver a sumar la unidad al resultado final.

Puedes realizar estos pasos con todas las unidades. Así, con uniades de

  • masa: t,kg,g,…\mathrm{t}, \mathrm{kg}, \mathrm{g}, \ldots

  • longitud: km,m,cm,…\mathrm{km},\mathrm{m},\mathrm{cm},\ldots

  • volumen: l,ml,…\mathrm{l}, \mathrm{ml}, \ldots

  • y tiempo: h,min,s,…\mathrm{h}, \mathrm{min}, \mathrm{s}, \ldots

Aquí todo tiene sentido, es decir, el cálculo es lógico y puedes hacer algo con el resultado.

Beispielcálculo lógico

  • 3m+4m=7m3\mathrm{m}+4\mathrm{m}=7\mathrm{m}

  • 15ml−10ml=5ml15\mathrm{ml}-10\mathrm{ml}=5\mathrm{ml}

  • 7min+4min−10min=1min7\mathrm{min}+4\mathrm{min}-10\mathrm{min}=1\mathrm{min}

Multiplicar unidades

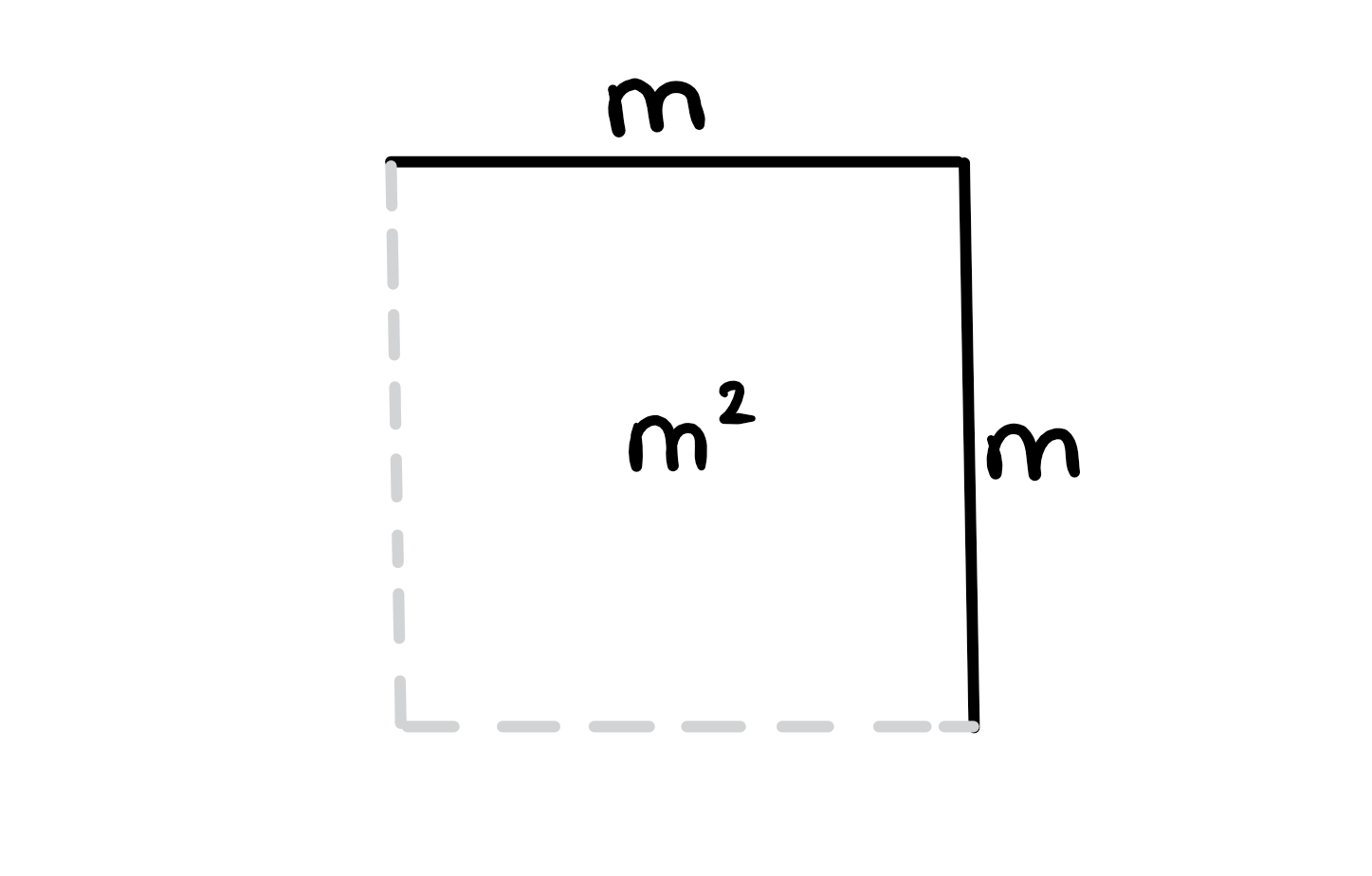
Al multiplicar unidades, la mejor manera de visualizar el concepto es calculando el área. Por ejemplo, si tienes una baldosa de suelo con una longitud de borde de 1m1\mathrm{m}, calcula: 1m⋅1m=1m2\mathrm{m}\cdot1\mathrm{m}=1\mathrm{m}^2

y así se obtiene el área de la baldosa, a saber =1m2=1\mathrm{m}^2.

O visto de otra manera: 1⋅1⋅m⋅m=1m21⋅1⋅\mathrm{m}⋅\mathrm{m}=1\mathrm{m}^2.

Este razonamiento puede continuar por ejemplo multiplicando con m\mathrm{m} o tambien con m2\mathrm{m}^2 para obtener nuevas medidas. Esto se ve de la siguiente forma:

Beispielpara obtener nuevas medidas

  • 1m2⋅1m=1m31\mathrm{m}^2\cdot1\mathrm{m}=1\mathrm{m}^3

  • 1m2⋅1m2=1m41\mathrm{m}^2\cdot1\mathrm{m}^2=1\mathrm{m}^4

Después, se puede volver a realizar este cálculo como en el caso anterior y llegar así a todas las posibilidades imaginables. Incluso m1000\mathrm{m}^{1000} es posible. Afortunadamente, no necesitas algo así todavía ;-)

En principio, esto es posible con todas las unidades que ya se indicaron en la sección de sumar/restar unidades. Es posible con kg\mathrm{kg}, m\mathrm{m}, también con indicaciones de tiempo como min\mathrm{min} y s\mathrm{s}.

Vorsicht

Sin embargo, aquí no siempre todo tiene sentido. Esto significa que, al menos en matemáticas, no se calcula con kg2\mathrm{kg}^2.

A partir de ahí puedes ver rápidamente si has calculado o convertido correctamente o si se ha producido un error.

superficie de metro cuadrado

Ejemplo

        Primero elige una unidad para hacer los caˊlculos: aquıˊ tomamos metros.        ↓200dm⋅10m2⋅0,1km=?Primero decide una unidad. Aquıˊ tomamos metros.        ↓20m⋅10m2⋅100m=?         Considera ahora coˊmo podrıˊas multiplicar primero           20m y 100m. Deja por el momento el 10m2.        ↓2000m2⋅10m2=?         Si m⋅m=m2, queˊ resulta entonces sim2⋅m2?        ↓20000m4\;\;\;\;\color{ff6600}\text{Primero elige una unidad para hacer los cálculos: aquí tomamos metros.}\\ \;\;\;\;\downarrow\\ \color{#000}200 \mathrm{ dm}\cdot10 \mathrm{ m}^2\cdot 0{,}1\mathrm{ km}=\text{?}\\ \color{ff6600}\text{Primero decide una unidad. Aquí tomamos metros.}\\ \;\;\;\;\downarrow\\ \color{#000}\\20\mathrm{ m}\cdot10\mathrm{ m}^2\cdot100\mathrm{ m}=\text{?}\\ \;\;\;\;\ \color{ff6600}\text{Considera ahora cómo podrías multiplicar primero }\\ \;\;\;\;\; 20\mathrm{ m} \text{ y } 100\mathrm{ m}\text{. Deja por el momento el } 10\mathrm{ m}^2.\\ \\ \;\;\;\;\downarrow\\ \color{#000} 2000\mathrm{ m}^2\cdot10\mathrm{ m}^2=\text{?}\\ \;\;\;\;\ \color{ff6600}\text{Si } \mathrm{ m}\cdot \mathrm{ m}=\mathrm{ m}^2,\text{ qué resulta entonces si} \mathrm{ m}^2\cdot\mathrm{ m}^2\text{?}\\ \\ \;\;\;\;\downarrow\\ \color{#000} 20000\mathrm{ m}^4

Dividir unidades

Al dividir las unidades, es importante reducirlas al máximo. Es mejor escribir el cálculo como una fracción. Esta es la forma más fácil de ver lo que se puede reducir y lo que no. Aquí también es importante primero convertir todo a un tamaño uniforme.

Ejemplo

Ejercicio: ¿Cuál es el ancho de un rectángulo con área A=10  m2A= 10\;\mathrm{m^2}y longitud l=5m\mathrm{l}=5\mathrm{m}?

A=l⋅b        Cambia el orden para obtener el ancho b.        ↓⇒b=Al        Ahora inserta los valores.        ↓b=10m25m        Ahora piensa en queˊ unidad debe salir.        Correcto, la anchura se mide en metros.        Eso tambieˊn es loˊgico, pues m2m=m⋅mm=m        ↓b=2mA=\mathrm{l}\cdot\mathrm{b}\\ \;\;\;\; \color{ff6600}\text{Cambia el orden para obtener el ancho b.}\\ \;\;\;\;\downarrow\\ \color{#000} \Rightarrow \mathrm{b}=\dfrac{A}{\mathrm{l}}\\ \;\;\;\; \color{ff6600}\text{Ahora inserta los valores.}\\ \;\;\;\;\downarrow\\ \color{#000} \mathrm{b}=\dfrac{10\mathrm{ m^2}}{5\mathrm{m}}\\ \;\;\;\; \color{ff6600}\text{Ahora piensa en qué unidad debe salir.}\\ \;\;\;\; \text{Correcto, la anchura se mide en metros.}\\ \;\;\;\; \text{Eso también es lógico, pues }\frac{\mathrm{m}^2}{\mathrm{m}}=\frac{\mathrm{m}\cdot \mathrm{m}}{\mathrm{m}}=\mathrm{m}\\ \;\;\;\;\downarrow\\ \color{#000}\color{#000} \mathrm{b}=2\mathrm{m}

Lista de verificación

Vorgehen

  1. Busca unidades uniformes

  2. Investiga tu operación aritmética.

  3. Calcula inteligentemente. Presta atención a la reducción/multiplicación de tus cantidades.

Caso especial: posiciones decimales

Puede ser que un ejercicio no se realice sólo con números enteros. También puede haber decimales. Si te enfrentas a una tarea de este tipo, definitivamente no debes cerrar tu cuaderno rápidamente.

BeachteEs muy sencillo:

Convierte todas las cantidades a la unidad más pequeña para evitar comas innecesarias. Luego, sigue calculando como has aprendido anteriormente. Al final, simplifica el resultado final convirtiendo de nuevo a una unidad mayor.

Ejemplo

        Unifica tus taman˜os convirtiendo a la unidad maˊs pequen˜a.        ↓13,5  dm+12  cm=135  cm+12  cm        Como las unidades son las mismas y se trata de una suma,        puedes calcular faˊcilmente el resultado.        ↓=147  cm=1,47  m                          =14,7  dm=1,47  m\;\;\;\; \color{ff6600}\text{Unifica tus tamaños convirtiendo a la unidad más pequeña.}\\ \;\;\;\;\downarrow\\ \color{#000} 13{,}5 \;\mathrm{ dm} + 12 \;\mathrm{ cm} = 135\;\mathrm{ cm}+12\;\mathrm{ cm}\\ \;\;\;\; \color{ff6600}\text{Como las unidades son las mismas y se trata de una suma,}\\ \;\;\;\; \text{puedes calcular fácilmente el resultado.}\\ \;\;\;\;\downarrow\\ \color{#000}=147 \;\mathrm{ cm}\\ =1{,}47\;\mathrm{ m}\\ \; \\\;\;\;\;\;\;\;\;\;\;\;\; = 14{,}7\;\mathrm{ dm}=1{,}47\;\mathrm{ m}

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel


Este contenido está licenciado bajo
CC BY-SA 4.0 → Información