Ejercicios con raíces cuadradas

El lado del cuadrado

Ya sabes:

$A_{c\acute{ı}rculo}=A_{cuadrado}=\mathrm{581,07}c{m}^2$

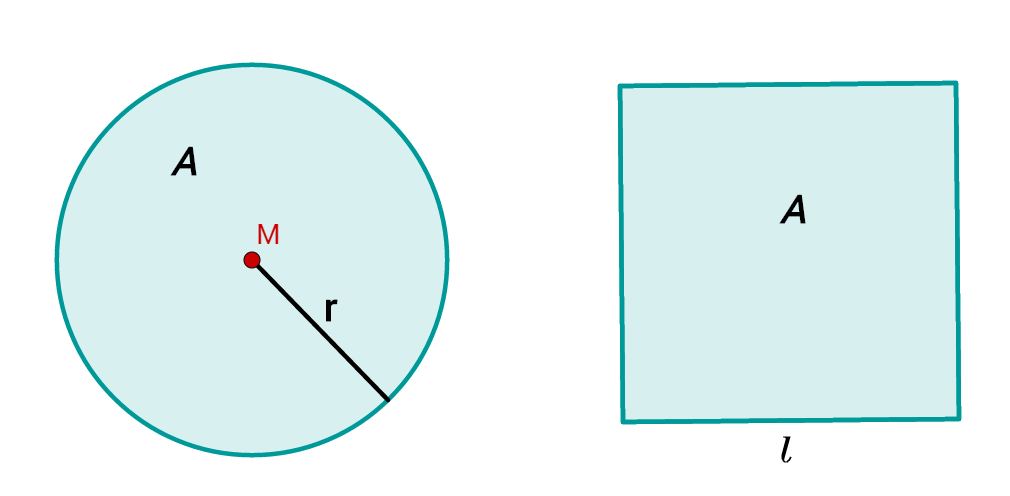
Ten a la mano la fórmula para calcular el área del cuadrado.

$A_{cuadrado}=l^2$

• aplica la raíz cuadrada utilizando el radical.

$\sqrt{A_{cuadrado}}=\pm l$

• Al resolver la raíz cuadrada obtienes dos soluciones.

$\sqrt{581.07c{m}^2}=\pm l$

Las dos soluciones que obtienes son:

• $l_{soluci\acute{o}n1}=-\mathrm{24,11}cm$

• $l_{soluci\acute{o}n2}=\mathrm{24,11}cm$

Atención: En el contexto del cuadrado, sólo una de las soluciones parece tener sentido.

Como la longitud del lado del cuadrado no puede ser negativa, la solución correcta es: $l=24.11cm$