Fórmula cuadrática para resolver ecuaciones de segundo grado (ecuación cuadrática)

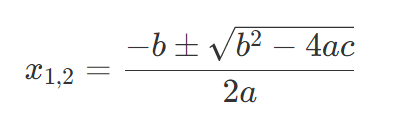
Fórmula cuadrática

Las soluciones de una ecuación cuadrática $\textcolor{ff6600}{a}x^2+\textcolor{009999}{b}x+\textcolor{cc0000}{c}=0$ son las siguientes

Número de soluciones posibles

El número de soluciones de una ecuación cuadrática de la forma $ax^2+bx+c=0$ depende del discriminante $D=b^2-4ac$.

El discriminante es exactamente el término que está debajo de la raíz en la fórmula gereral.

Una ecuación cuadrática tiene:

• dos soluciones, si $D>0$

• exactamente una solución, si $D=0$

• ninguna solución, si $D<0$.

Resolver una ecuación cuadrática con la fórmula cuadrática

Para resolver una ecuación cuadrática con la fórmula cuadrática, tienes que tomar los coeficientes $a$, $b$ y $c$ de la forma $ax^2+bx+c=0$ y luego sustituirlos en la fórmula cuadrática.

Procedimientos con tres ejemplos

Ejemplo 1

Procedimiento:

$x_{1{,}2}=\dfrac{-3\pm\sqrt{3^2-4\cdot2(-5)}}{2\cdot2}= \dfrac{-3\pm\sqrt{49}^{2\cdot2}}{4}$

$\displaystyle \Rightarrow x_1=\frac{-3+7}{4}=\frac{4}{4}=1 \\ \displaystyle \Rightarrow x_2=\frac{-3-7}4=d\frac{-10}{4}=-\dfrac{5}{2}$

Ejemplo 2

Procedimiento:

$x_{1{,}2}=\dfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot1\cdot1}}{2\cdot1}= \dfrac{2\pm\sqrt{0}}{2} \\ \displaystyle \Rightarrow x=\frac{2}{2}=1$

Solución alternativa: Aquí también se puede aplicar una fórmula binomial.

$x^2−2x+1=(x−1)^2=0\displaystyle \Rightarrow x=1$

Ejemplo 3

Procedimiento:

$x_{1{,}2}=\dfrac{4\pm\sqrt{(4)^2-4\cdot3\cdot5}}{2\cdot3}= \dfrac{-4\pm\sqrt{-44}}{6} \\ \displaystyle \Rightarrow x=\text{no hay solución}$

Vídeo ejemplo

Encontrar los coeficientes en casos más complicados

A menudo la ecuación cuadrática no está dada en la forma $ax^2+bx+c=0$.

Para llegar a esta forma, se suele proceder de la siguiente manera:

Ejemplo:

Paso 1. Transformar la ecuación: Primero hay que transformar la ecuación cuadrática para que haya un 0 en uno de los dos lados.

$5x+3x^2−7 =​2x^2+3x \ \textcolor{009999}{∣ \ ​−(2x^2+3x)\ \text{pasar al otro lado del signo =}} \\ 5x+3x^2−7​−2x^2+3x=0$

Paso 2. combinar términos del mismo tipo: Resume todos los términos cuadráticos (sumandos con $x^2$), todos los términos lineales (todos los sumandos con x) y todos los términos constantes (números reales).

$3x^2−2x^2+5x−3x−7​=0​ \\ x^2+2x-7=0$

Paso 3. Lee e identifica los coeficientes: ten en cuenta la formula para esto.

• $\boldsymbol {\textcolor{ff6600}{a}}$ es el factor que precede $\boldsymbol x^2$

• $\boldsymbol{\textcolor{009999}{b}}$ es el factor que precede $\boldsymbol x$

• los restantes sumandos que no contienen $\boldsymbol x$ se suman a $\boldsymbol{\textcolor{cc0000}{c}}$.

$x^2+2x-7=0$

$\textcolor{ff6600}{a}=1, \textcolor{009999}{b}=2,\textcolor{cc0000}{c}=-7$

Paso 4. insertar en la fórmula cuadrática: Ahora tienes que insertar los valores en la fórmula cuadrática.

Los coeficientes no siempre tienen que ser números, también pueden contener parámetros. Puedes leer más sobre esto en el artículo Parámetros en ecuaciones cuadráticas.

Derivación de la fórmula cuadrática

Para derivar la fórmula cuadrática, resuelve la ecuación cuadrática general utilizando complementos a la ecuación.

1- llevamos $c$ al lado derecho restando $c$:

2- dividimos la ecuación por $a$ y formamos el factor al ampliar $x$ simplemente con un 2:

3- ahora sigue utilizando complementos a la ecuación: sumamos en ambos lados $\textcolor{ff6600}{\left( \dfrac{b}{2a} \right)^2}$

4- aplica la 1ª fórmula del binomio para escribir el lado izquierdo como un cuadrado:

5- ahora podemos resolver para $x$ sacando primero la raíz:

6- lleva entonces $\frac{b}{2a}$ al otro lado:

En principio, hemos terminado, tenemos una fórmula de solución. Sin embargo, todavía no tiene el aspecto deseado. Para ello, reformulamos el término en la raíz

y obtener para el lado derecho ...

Con esto hemos derivado la fórmula cuadrática: $x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

Fórmula pq para resolver ecuaciones cuadráticas (Coeficiente principal uno en la ecuación completa)

La fórmula pq se utiliza como alternativa a la fórmula cuadrática. También se utiliza para resolver una ecuación cuadrática y es algo más fácil de recordar. Un requisito previo, sin embargo, es que el coeficiente del sumando cuadrático $a=1$. Para ello pueden ser necesarias transformaciones.