Distancia de un punto a una recta

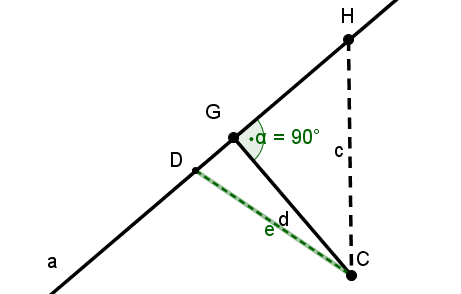
Buscamos la distancia del punto $CC$ a la recta $aa$. Si observamos el dibujo de la derecha, vemos que el segmento entre $GG$ y $CC$, también llamado $[GC][GC]$, es la distancia más corta que buscamos. (Esto se reconoce por el ángulo recto entre la recta $aa$ y el segmento $[GC][GC]$). Los segmentos $[DC][DC]$ y $[HC][HC]$ también son distancias, pero son más largas que $[GC][GC]$ y, por tanto, no son la distancia que buscamos.

La recta $GCGC$ también se llama perpendicular.

Medir con una escuadra fija

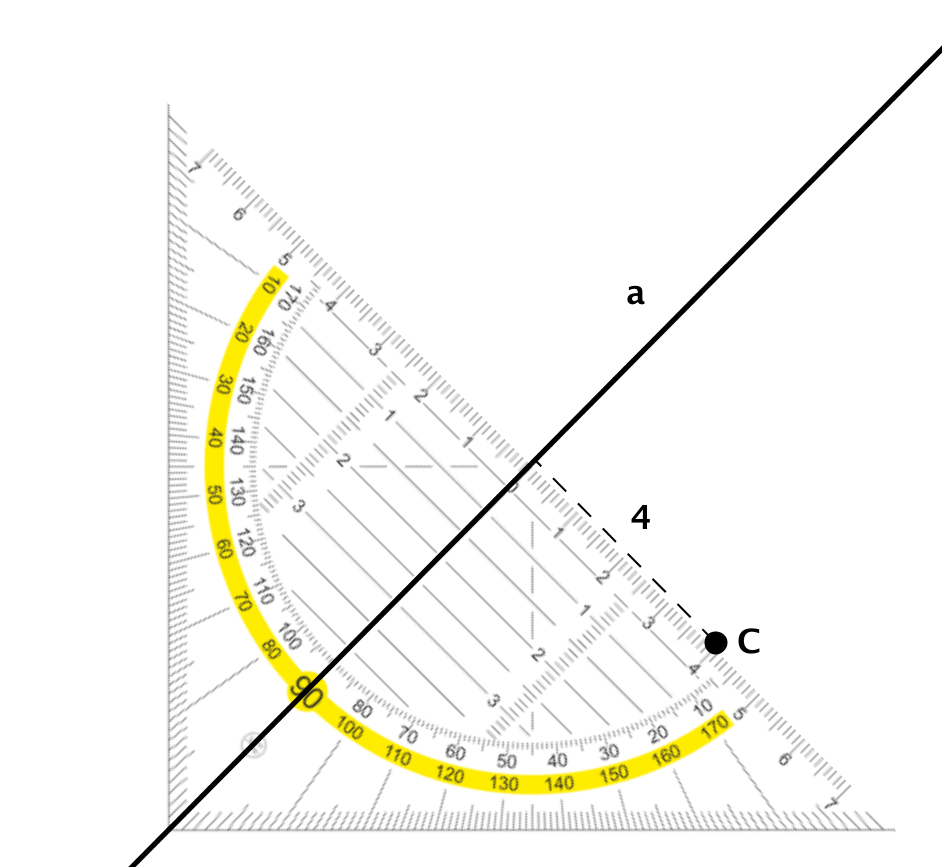
1. Coloca la escuadra sobre la recta de forma que el eje de la escuadra, que pasa por el cero, quede exactamente sobre la recta.

2. Ahora mueve la escuadra a lo largo de la línea recta de modo que el punto $CC$ se encuentre en la regla numerica de la escuadra.

3. Ahora se puede leer la distancia del punto a la línea recta en la escuadra.

4. En el ejemplo de la derecha, la distancia es de 4 cm.

Construcción de la conexión más corta del punto con la recta

Se ha dado: Recta $aa$ y punto $CC$

Ahora determina la distancia de la siguiente manera:

1. Dibuja una circunferencia con centro $CC$ de modo que la circunferencia intersecte a la recta en dos puntos $EE$ y $FF$.

2. Luego construye una mediatriz a los puntos $EE$ y $F\mathrm{.}F.$

3. El punto de intersección de la recta con la perpendicular central se designa como $GG$.

4. Ahora se puede medir la distancia entre $GG$ y $CC$.

En el siguiente applet se muestra de nuevo la construcción paso a paso. Simplemente arrastra el deslizador $bb$ hacia la derecha.