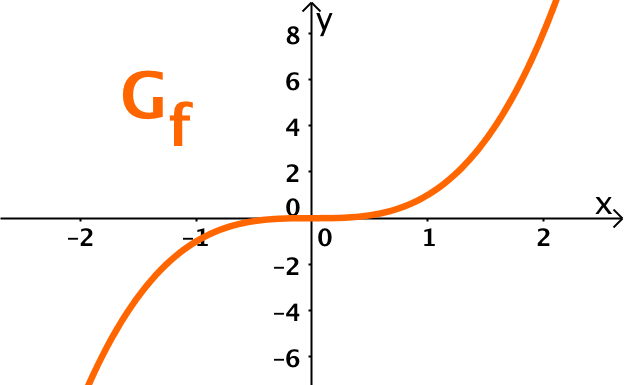Gráfica de una función

Puede considerarse formalmente como el conjunto de puntos para los que

• la coordenada $xx$ vienen determinados por el dominio de la función y

• la coordenada $yy$ es el rango ( también llamado conjunto final o contradomino), el valor que da la función de la coordenada x.

Símbolos y notación cuantitativa

Para la gráfica de una función $ff$ se escribe $G_{f}G\_f$. Como conjunto, $G_{f}G\_f$ puede escribirse así:

$G_f=\{(x,y)\mathrm{\mid }x\in D_f\text{ y }y=f(x)\}G\_f\; =\; \backslash \{(x,y)|x\backslash in\; D\_f\; \backslash \; \backslash \; \backslash \; \backslash text\{y\}\; \backslash \; \backslash \; y=f(x)\backslash \}$

también

$G_f=\{(x,f(x)\mathrm{\mid }x\in D_f)G\_f=\backslash \; \backslash \{(x,\; \backslash \; f(x)|x\backslash in\; D\_f)$

Dibuja gráficos con una tabla de valores

La forma más directa de dibujar una gráfica es calcular el mayor número posible de puntos de la misma. Esto se hace así:

• Selecciona cualquier número como coordenada x

• inserta la coordenada x en el término de la función

• el resultado $f(x)f(x)$ es entonces la coordenada y

• introduce el punto $(x,f(x))(x,\; f(x))$ en un sistema de coordenadas

Una vez que hayas dibujado algunos puntos de la gráfica, puedes dibujar la gráfica continua.

Ejemplo

$f(x)={\displaystyle \frac{x^2}{2}}-4f(x)=\backslash dfrac\{x^2\}\{2\}-4$

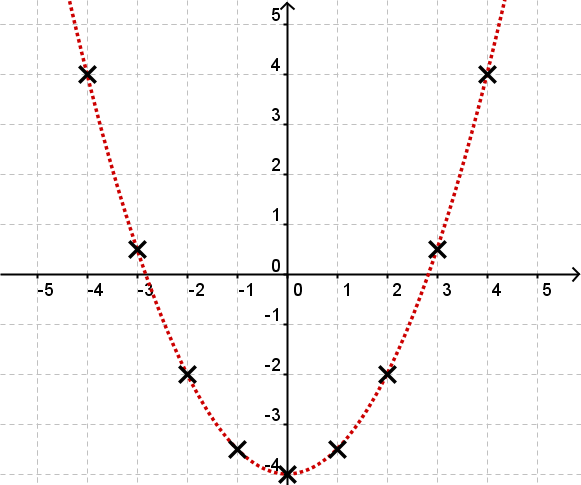
Algunos puntos se introducen aquí en una tabla de valores:

Ahora puedes dibujar la gráfica orientándote en estos puntos. Se ve así.

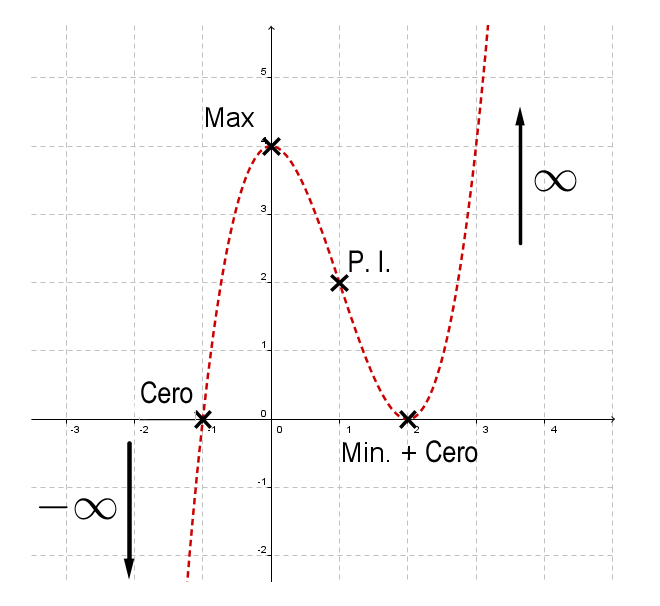
La discución de la curva en la gráfica

Si ya has realizado una investigación de la curva de la función, es aconsejable dibujar los puntos importantes de la gráfica:

• mínimo (Max)

• máximos (Min)

• ceros (Cero)

• puntos de inflexión (P.I.)

• terrazas (Ter)

Con estos puntos como puntos de apoyo y los valores límite contra $\pm \mathrm{\infty }\backslash pm\backslash infty$, suele ser mucho más fácil trazar la gráfica que con puntos seleccionados arbitrariamente.