Ecuación cuadrática o de segundo grado
Una ecuación cuadrática o de segundo grado es una ecuación que se puede transformar en la forma:
teniendo en cuenta que ∖{} y
Ejemplos de ecuaciones cuadráticas:
y tambien:
, ya que la ecuación se puede transformar en .
ya que la ecuación se puede transformar en
La mayoría de las veces se requiere encontrar la solución de una ecuación cuadrática. Lo mejor es reordenar la ecuación para que sólo esté en un lado de la ecuación.
Cantidad de soluciones
Puedes averiguar la cantidad de soluciones de forma gráfica o por cálculo.
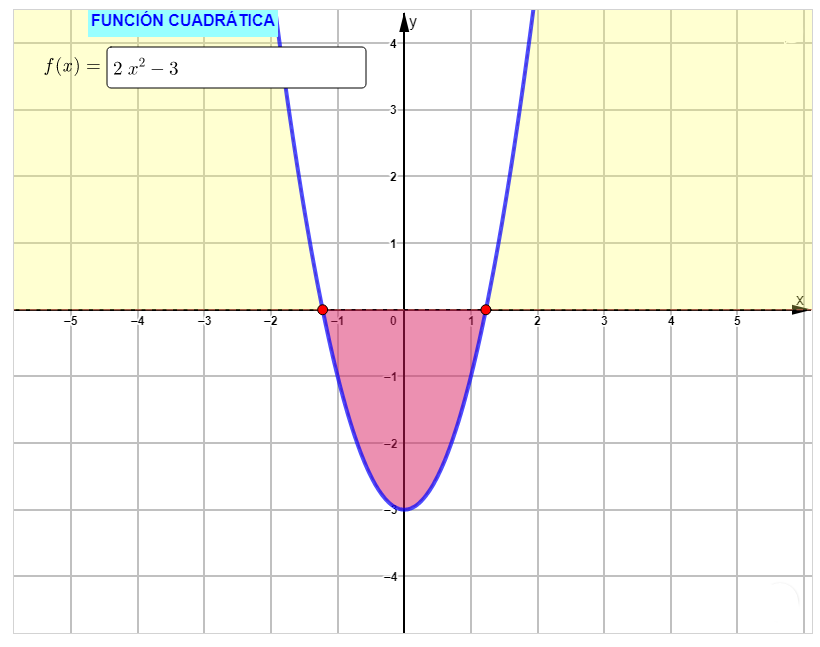
Gráficamente, puedes dibujar la función y luego leer el número de ceros en la funcion. Lo siguiente se aplica a los ceros de una parábola:

Si la parábola está completamente por encima del eje o completamente por debajo, entonces no hay solución.
Si el vértice de la parábola se encuentra en el eje , entonces hay exactamente una solución.
Si la parábola pasa por el eje (dos veces), entonces hay exactamente dos soluciones.
Puedes calcular la cantidad de soluciones calculando el discriminante:
: no hay solución
: exactamente una solución
: exactamente dos soluciones
Fórmulas de solución
Para saber cuál es la solución de la ecuación cuadrática, siempre puedes utilizar la fórmula cuadrática y la fórmula pq.
Este no es siempre el método más fácil, pero más sobre esto en la sección "Resolución inteligente de ecuaciones cuadráticas".
Fórmula cuadrática
Una técnica comúnmente utilizada para resolver ecuaciones cuadráticas es la fórmula cuadrática.
Determina la solución de una ecuación de la forma utilizando la fórmula:
Ejemplo:
Encuentra la solución para .
Solución:
Lee los valores de , y y sustitúyelos en la fórmula cuadrática:
Fórmula pq
Puedes aplicar la fórmula pq a las ecuaciones cuadráticas de la forma donde
La solución de la ecuación es entonces
¿Tienes un factor antes de ?
No pasa nada, también puedes utilizar la fórmula pq.
Sin embargo, primero hay que dividir toda la ecuación por el factor previo.
Ejemplo:
Resuelve la igualdad
Solución:
Como hay un factor de antes de , primero hay que dividir toda la ecuación por , así:
Ahora aplica la fórmula pq al término .
Lee los valores y para ello:
Teorema de Vieta
El teorema de Vieta es un método de solución que permite adivinar los ceros de una función por ensayo y error. Por tanto, el método sólo es adecuado si las soluciones de la ecuación son sencillas. Sin embargo, también puede utilizar el método para comprobar rápidamente los ceros de la función calculados.
Según el teorema de Vieta, las soluciones y de una ecuación de la forma cumplen las siguientes condiciones:
Ejemplo:
Resuelve la igualdad
Solución:
Lee los valores de y . Aquí y .
Ahora busca los números y que satisfacen las siguientes ecuaciones:
Si se consideran sólo números enteros, sólo para
y o
y
Prueba si uno de los pares también cumple la primera condición:
,
y
Para y se cumplen ambas condiciones. Así que las soluciones de la ecuación son y .
Nota: Soluciones como y difícilmente se pueden adivinar con este método. Para ello se necesitan otros métodos de solución.
Solución eficaz de ecuaciones cuadráticas
Dependiendo de su forma, las ecuaciones cuadráticas también pueden resolverse mucho más fácilmente que con la fórmula cuadrática o la fórmula pq. Aquí depende de la forma en que se encuentren.
Aquí se pueden distinguir o considerar las siguientes formas o expresiones:
(forma estándar mixta)
Forma estándar
Puedes reconocer rápidamente las ecuaciones en forma estándar por el hecho de que falta el sumando "con ". Las resuelves sacando la raíz.
Ten en cuenta que no hay solución cuando tomas la raíz de un número negativo. Con un número positivo, siempre hay exactamente dos soluciones: una de ellas es negativa y la otra positiva.
Ejemplo:
resuelve
Solución:
Producto cero
Un producto cero es un producto cuyo resultado es . Los productos cero son, por ejemplo, las siguientes ecuaciones:
Si tu ecuación tiene esta forma o puede transformarse fácilmente en forma, puedes leer las soluciones de la ecuación.
Ejemplo:
resuelve las igualdades:
a)
b)
Solución para a:
Un producto es cero si uno de los factores es cero. Por tanto, deben ser o .
Por tanto, la ecuación se cumple para y .
Solución para b:
Puedes transformar la ecuación en un producto cero:
Por tanto da, o .
Por tanto, las soluciones de la ecuación son y .
Ecuaciones en forma del vértice
Las ecuaciones cuadráticas en forma de vértice también pueden transformarse en una ecuación cuadrática de forma estandar mixta con la ayuda de las fórmulas binomiales y luego resolverse como se ha descrito anteriormente. Sin embargo, la técnica de cálculo hacia atrás es mucho más fácil en este caso:
Ejemplo:
resuelve
Solución:
Still want more?
You can find more content on this topic here: