1 Descripción general

Contenido del curso
En este curso aprenderás a calcular la longitud de un vector o el ángulo entre dos vectores. Entre otras cosas, se introducen términos como el producto escalar. Además, se aborda el cálculo del área de un triángulo con la ayuda de determinantes.
Conocimientos previos (en construcción)
Deberías haber entendido la definición de vector. Para repetirlo, puedes echar un vistazo al curso Introducción al concepto de vector (Vectores en el plano I).
Deberías ser capaz de calcular con vectores. Esto se trata en el curso Cálculo con vectores (Vectores en el plano II).
Puedes entender mejor el curso si ya conoces el teorema de Pitágoras.
Duración del curso
aprox. 3 horas
2 Producto escalar
El producto escalar es una especie de "multiplicación" de vectores cuyo resultado es un número real. Se escribe
Se determina de la siguiente manera:
Dados dos vectores:
y
Entonces
Ortogonalidad
Un vector es ortogonal a un vector si los dos vectores son perpendiculares entre sí, lo que se puede comprobar mediante el producto escalar de ambos vectores.
Si es igual a cero, entonces y son ortogonales entre sí. Es decir:
(Cuando, y )
Los vectores no siempre tienen que ser ortogonales entre sí.
Estos vectores se reconocen por el hecho de que su producto escalar no es igual a cero, es decir, sus representantes no están en ángulo recto.
Se aplica:
no es perpendicular a

Nota: No es importante que los vectores tengan un punto de pie común, porque puedes tomar simplemente sus representantes, que tienen sus puntos de pie en el origen (vectores de localización).
Por supuesto, nada cambia en el resultado del producto escalar, y mucho menos en el propio vector.
3 Ángulo
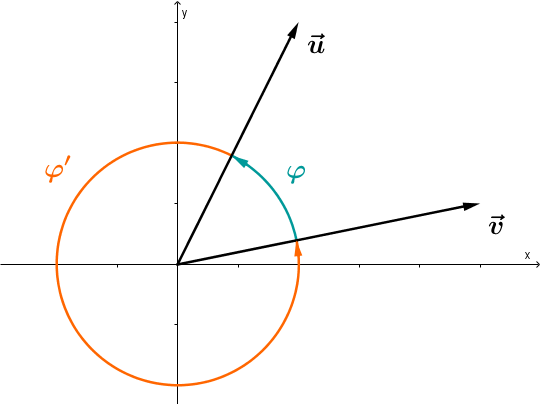
Ahora puedes determinar el ángulo entre dos vectores. Esto se hace siempre en sentido contrario a las agujas del reloj.
A la derecha en la gráfica puedes ver que hay dos posibilidades: El menor ángulo y el mayor ángulo . Sin embargo, normalmente sólo se da el ángulo menor.
Se aplica siempre: .
El cálculo del ángulo entre y es el siguiente:
respectivamente
Aquí el "∘" representa el producto escalar.
"" es la función coseno inversa: el arco coseno. Esto significa, en particular, que
El ángulo mayor se puede calcular así:
