Teorema de Tales - Arco Capaz
El arco capaz se utiliza para averiguar desde dónde una distancia en un ángulo determinado se ve.
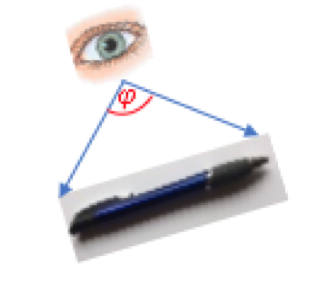
Ejercicio
En el applet opuesto, es una cuerda de la circunferencia alrededor de .
Los puntos , y se pueden mover. Haz clic en ellos y muévelos.
a) ¿Cómo se pueden mover los puntos en el plano?
b) ¿En qué posición aparece la cuerda para las diferentes posiciones de los puntos?
El teorema de la circunferencia de Tales
Si la cuerda es el diámetro de una circunferencia, los dos arcos de capaz son semicírculos y cada uno capta un ángulo de borde de .
Desde cualquier punto de la circunferencia, cada diámetro aparece en el ángulo de visión de
Excepciones: Los respectivos puntos finales de los diámetros.
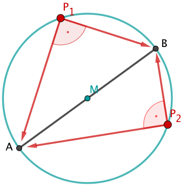
Teorema de Tales - Arco Capaz
Sea una cuerda del círculo que no es un diámetro. Entonces, aplica:
Todos los ángulos de los vértices del arco más largo son iguales.
El ángulo del borde es la mitad del ángulo central:
El ángulo del vértice es tan grande como el ángulo de la tangente de la cuerda:
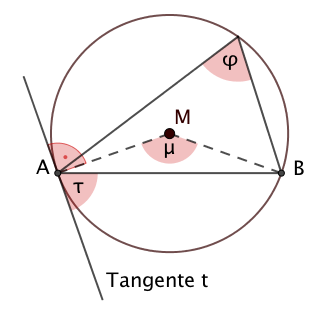
Para cada dimensión de ángulo del vértice del arco menor se aplica:
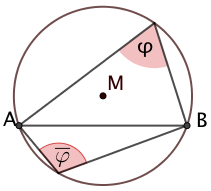
El par de arcos de capaz
El teorema del ángulo capaz afirma que una línea aparece desde cada punto de su arco de capaz con el mismo ángulo de visión.
Como el tamaño de un ángulo no cambia cuando se refleja en una línea recta, el ángulo de visión en la línea no cambia cuando el arco capaz se refleja en la línea de la cuerda.
El par de arcos capaz, es entonces el conjunto de todos los puntos (el llamado "lugar geométrico") a partir del cual la línea aparece en el ángulo dado.
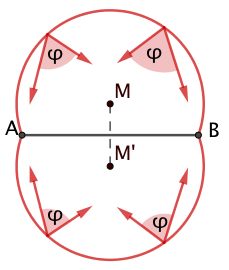
Construcción del arco capaz
Ejercicio:
Construye el par de arcos capaz hasta el ángulo límite .
Acá lo puedes observar en 6 pasos.
La construcción de la circunferencia tangente en el punto aplicando el ángulo cuerda-tangente de ya es decisiva en el 1º/2º paso. La perpendicular a la tangente lleva al centro de la circunferencia.
Paso 1

Paso 2

Paso 3

Paso 4

Paso 5

Paso 6

Exercises
Loading
Loading
Loading