Teorema de Tales
Según el teorema de Tales:
Si se construye un triángulo a partir de los vértices del diámetro de una círcunferencia (de Tales) y otro punto del arco, el ángulo en el punto del arco es un ángulo recto.
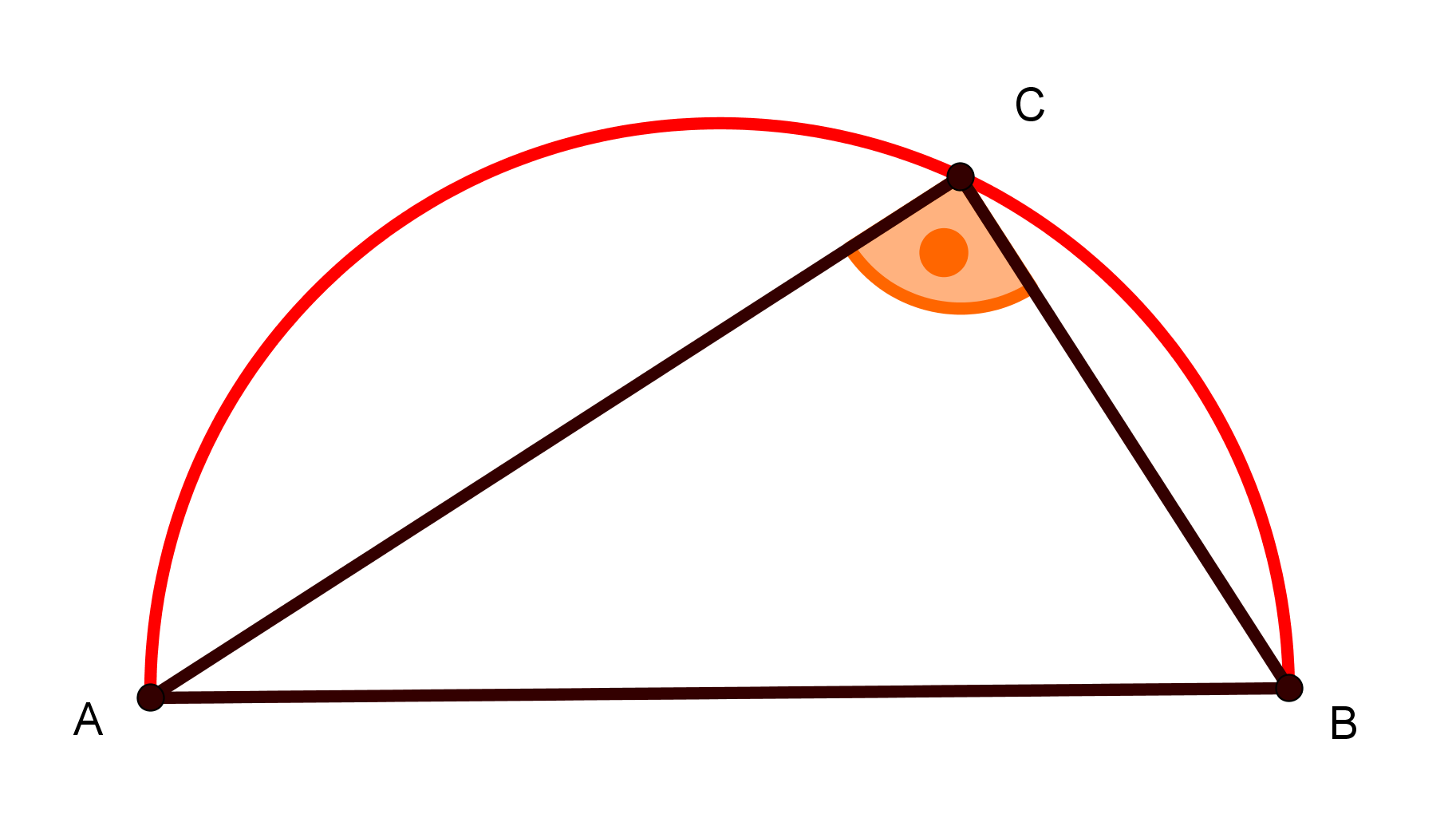
Pasos de Construcción
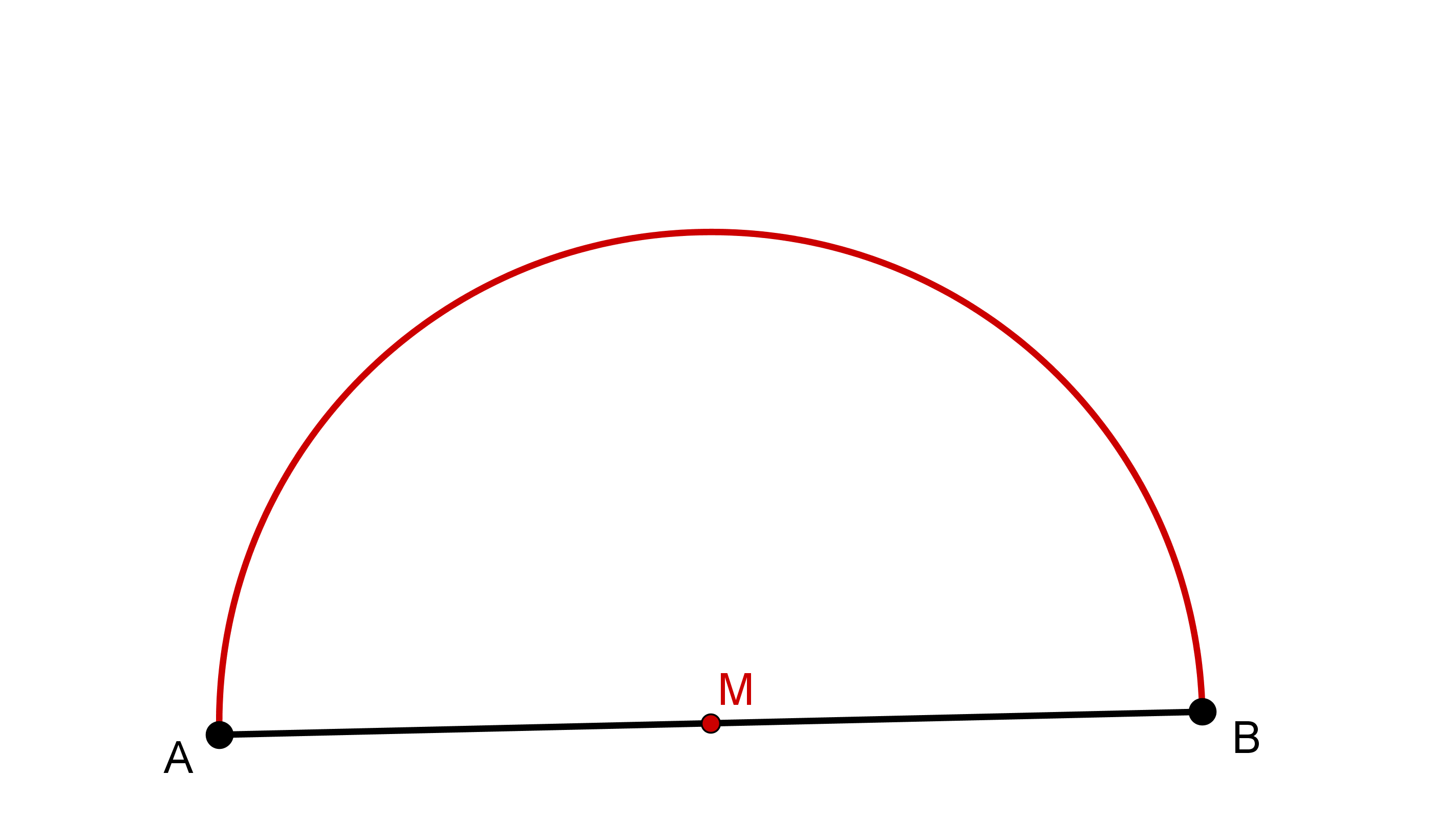
Empieza con una recta cualquiera (aquí: [AB]).

Construye ahora una circunferencia de Tales (aquí con centro ).
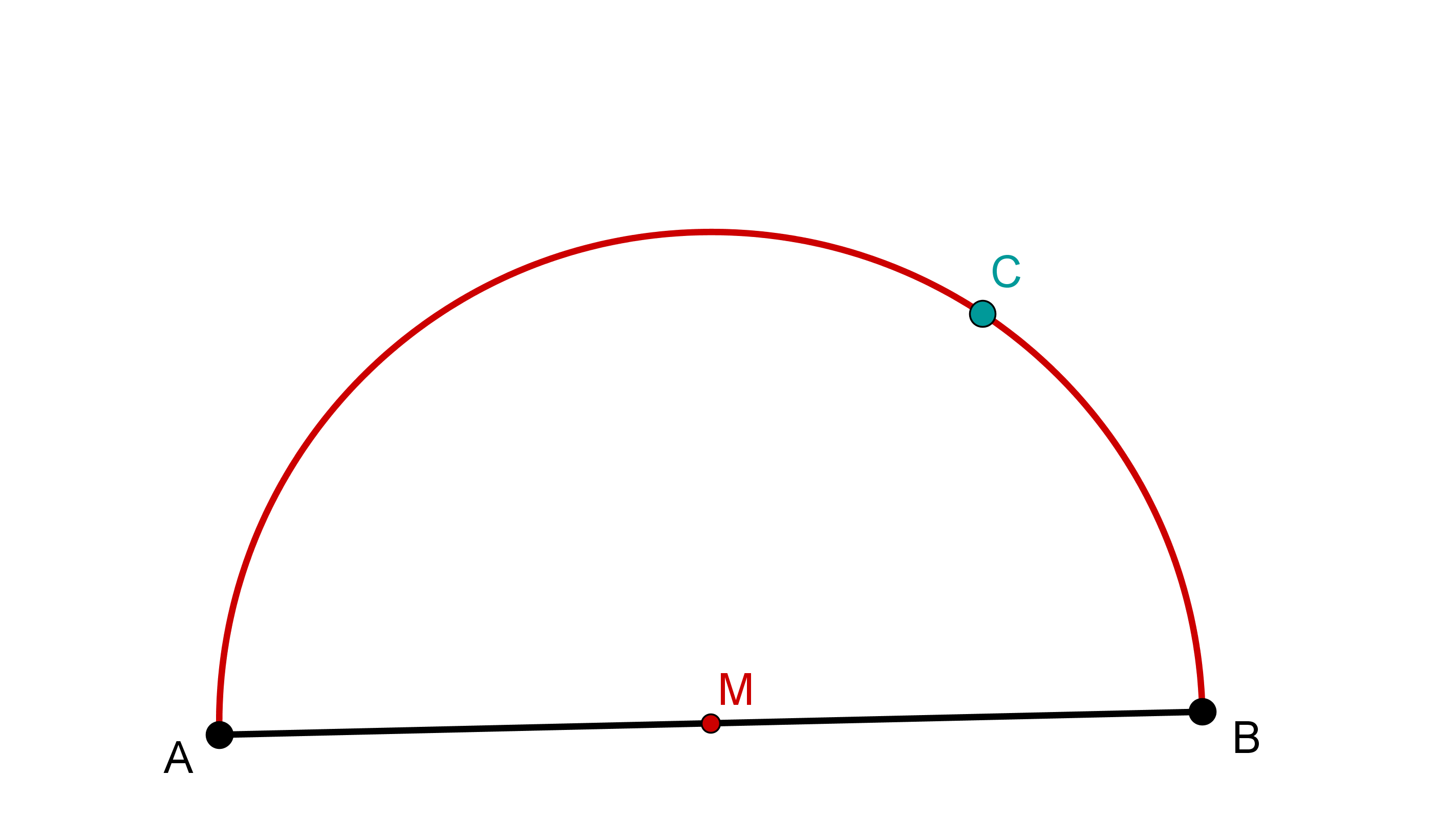
Ahora puedes marcar cualquier punto en el arco (aquí el punto ).
Ahora une los puntos , y para formar un triángulo.
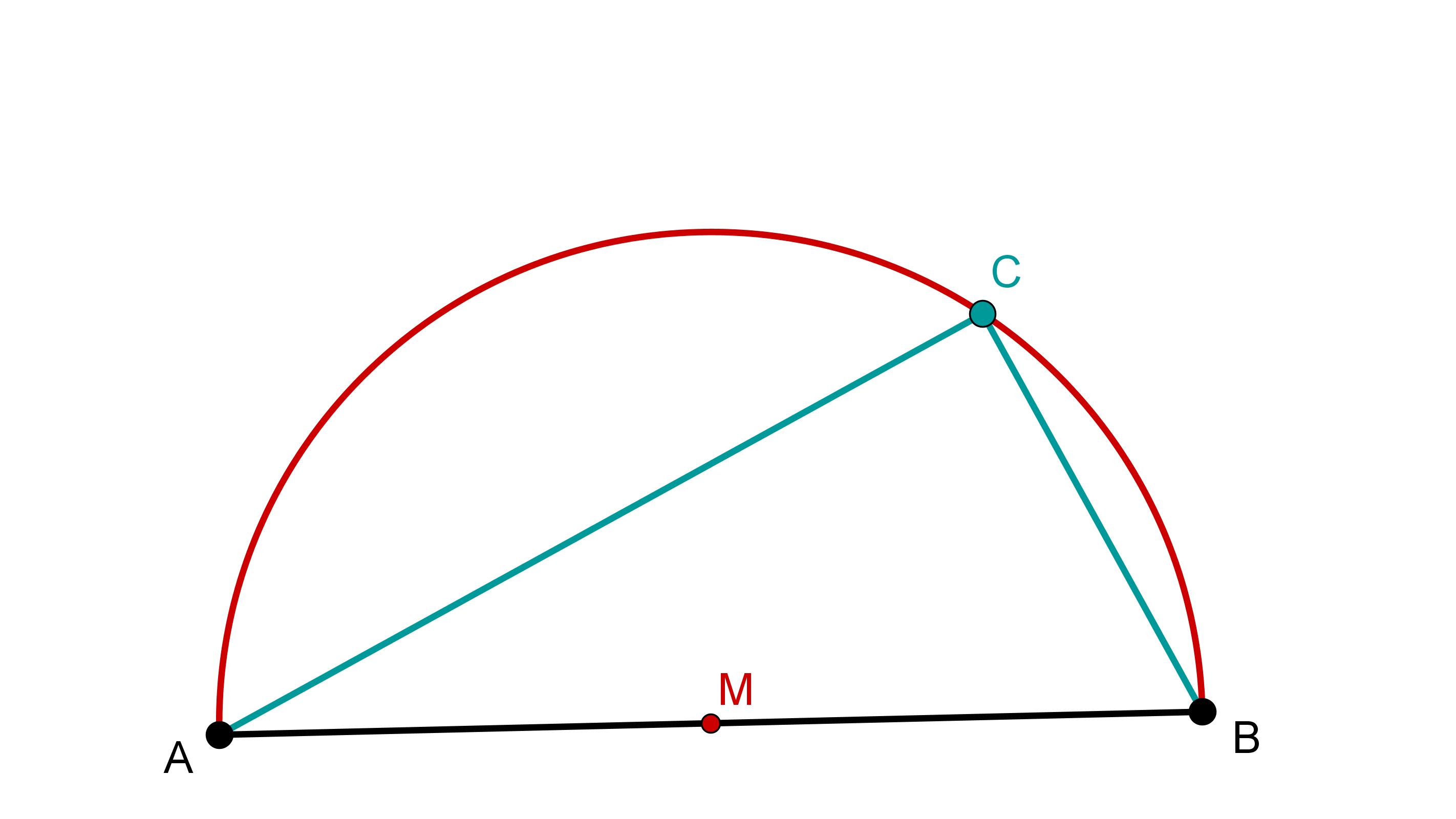
El ángulo es un ángulo recto.
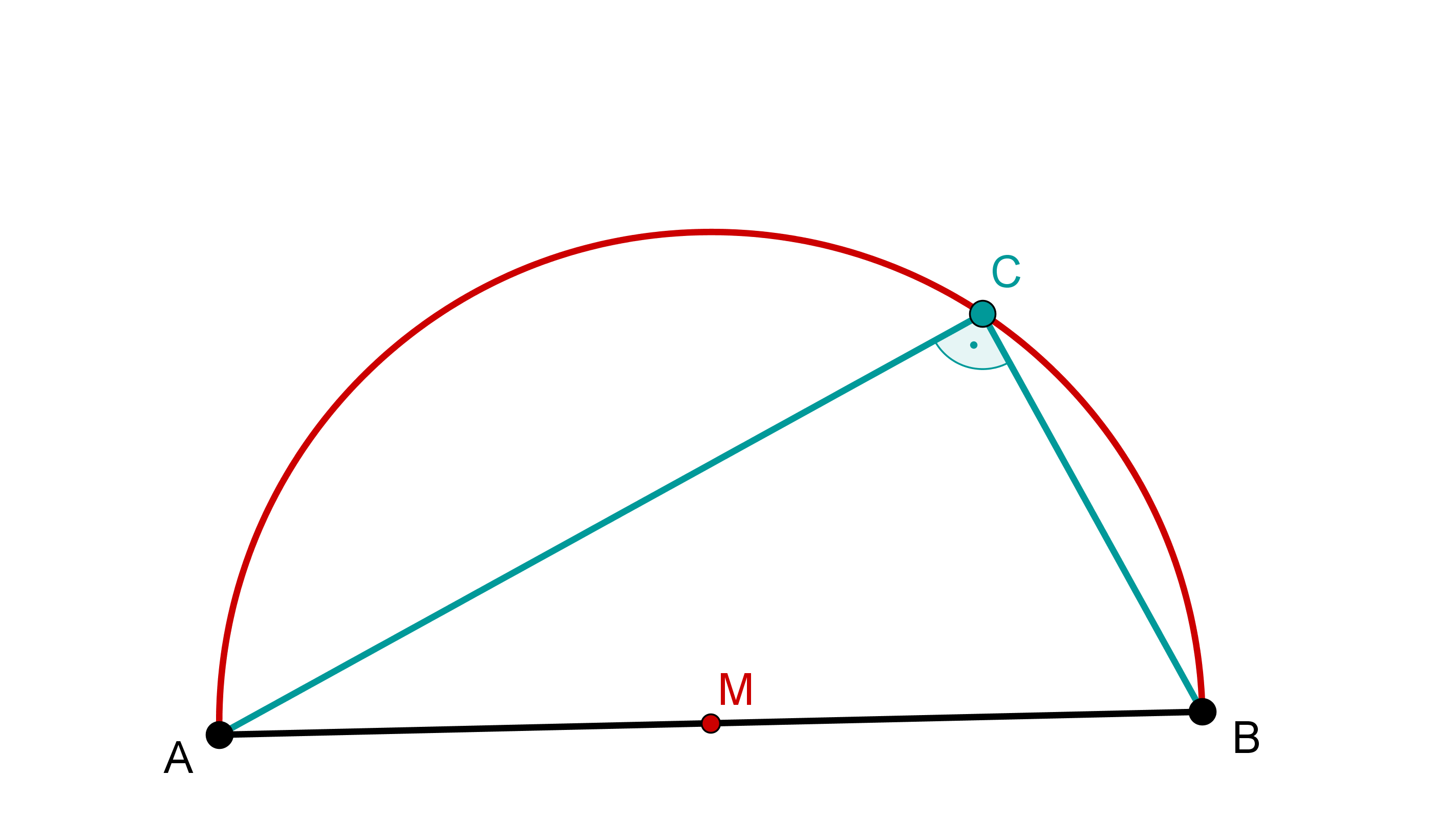
Puedes mover el punto (aquí: punto ) en la ilustración gráfica (applet) de la derecha como quieras y hacer lo mismo con él cada vez para comprobar la afirmación.
Aplicación
La circunferencia de Tales es útil para construir triángulos rectos.
También puede utilizarse para construir una tangente a una circunferencia que pase por cualquier punto fuera de la misma.
Inversión del teorema de Tales
También se aplica la afirmación inversa:
Aclaración: Prueba, Teorema de Tales
Primero dibuja un triángulo con la hipotenusa como el diámetro de una circunferencia y el tercer punto del triángulo en el arco de la circunferencia (aquí: punto ).
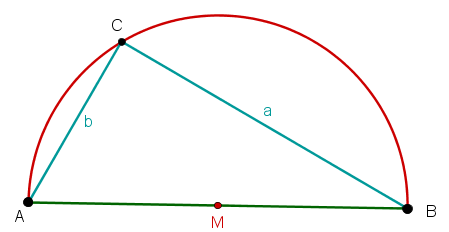
Además, introduce la línea bisectriz de la hipotenusa. Esto crea dos nuevos triángulos:
y
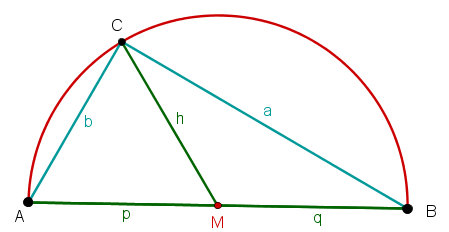
Ahora bien, ya se sabe que la suma de los ángulos interiores de un triángulo es .
Tanto en el triángulo como en los triángulos y
Por lo tanto:
Además:
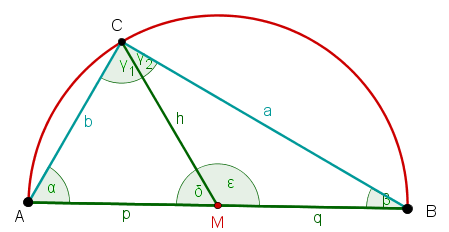
Los triángulos y son isósceles porque .
Por lo tanto:

Así es como se obtiene:
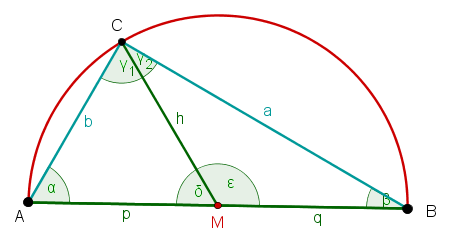
Esto demuestra que el ángulo es un ángulo recto, independientemente de cómo se elija el punto de la trayectoria en el arco capaz.