Período (de una fracción)

El período de un número decimal con infinitas cifras decimales es una secuencia de dígitos que se repite infinitamente.

Como signo para el período, se utiliza una línea horizontal sobre los dígitos, que se repiten.

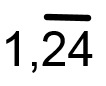
el periodo con el símbolo de la línea encima

Ejemplos	Con palabras el número decimal
La fracción $\frac{1}{3} = 0,3333333 = 0, 3$ tiene el período $3$ .	Cero coma período 3.
La fracción $\frac{16}{99} = 0,161616 = 0, 16$ tiene el período $16$ .	Cero coma período 16.
La fracción $\frac{1}{6} = 0,166666 = 0,1 6$ tiene el período $6$ (no el $16$ ).	Cero coma 1 período 6.
La fracción $\frac{2}{7} = 0,285714 = 0, 285714$ tiene el período $285714$ .	Cero coma período 285714.
La fracción $\frac{3}{4} = 0,75 = 0,75$ no tiene período.	Cero coma setenta y cinco.

Números decimales de periódo puro

Los números decimales periódicos puros son números en los que el período comienza directamente después de la coma.

Ejemplos

$0, 78$
$1, 7$
$8, 478$

Números decimales de periódo mixto

Los números decimales de período mixto son números periódicos en los que hay una o más cifras entre la coma y el período, es decir, el período no empieza directamente después de la coma.

Ejemplos

$0, 78$
$524,57 924$
$35,6 534$

Convertir un número decimal periódico en una fracción

Un número decimal periódico siempre se puede escribir como una fracción. Cómo pasar de la notación de números decimales a la notación de fracciones puede leerse en el artículo Conversión de números decimales a fracciones.

Teorema sobre la longitud de un período

Cada número decimal puede tener un período tan largo como máximo el denominador en la fracción correspondiente menos 1.

Ejemplos

La fracción $\frac{1}{7}$ tiene como máximo un periodo de longitud $6$ dígitos, ya que $7 - 1 = 6$ .	$\frac{1}{7} = 0. 142857$ tiene una longitud de período de $6$ dígitos.
La fracción $\frac{1}{17}$ tiene como máximo un periodo de longitud $16$ dígitos, ya que $17 - 1 = 16$ .	$\frac{1}{17} = 0. 0588235294117647$ tiene una longitud de período de $16$ dígitos.
La fracción $\frac{1}{3}$ tiene como máximo un periodo de longitud $2$ dígitos, ya que $3 - 1 = 2$ .	$\frac{1}{3} = 0. 3$ tiene una longitud de período de $6$ dígitos.

El último ejemplo muestra claramente que la frase sólo hace una declaración sobre la longitud máxima del período (y no sobre la longitud exacta del período).

Por cierto, el teorema se aplica en todos los sistemas de numeración. $0, {5 B}_{17}$ , por ejemplo, sería nuestro $\frac{1}{3}$ en el sistema heptadecimal (es decir Base 17).

Singularidad de la representación decimal

Estamos acostumbrados a que las matemáticas sean una ciencia exacta y, por tanto, inequívoca. Sin embargo, con la notación de fracción decimal surge una ambigüedad. Lo siguiente es cierto:

$0, 9 = 1$

Se puede representar el $1$ mediante dos números decimales diferentes: Por el conocido $1$ y por el $0, 9$ .

Muchos otros números, por supuesto, también tienen representaciones ambiguas como números decimales:

$2 = 1, 9$
$0,25 = 0,24 9$
etc.

Infinitos decimales no periódicos

También hay números decimales que tienen un número infinito de cifras decimales pero que no se repiten periódicamente. Estos números se llaman números irracionales. Están contenidos en los números reales.

Uno de los representantes más conocidos de estos números es el $π$ .	$π = 3.14159265358979323 \dots$

Atención:

¡Los números irracionales no pueden representarse como una fracción!

Este contenido está licenciado bajo
CC BY-SA 4.0 → ¿Qué quiere decir esto? serlo.org