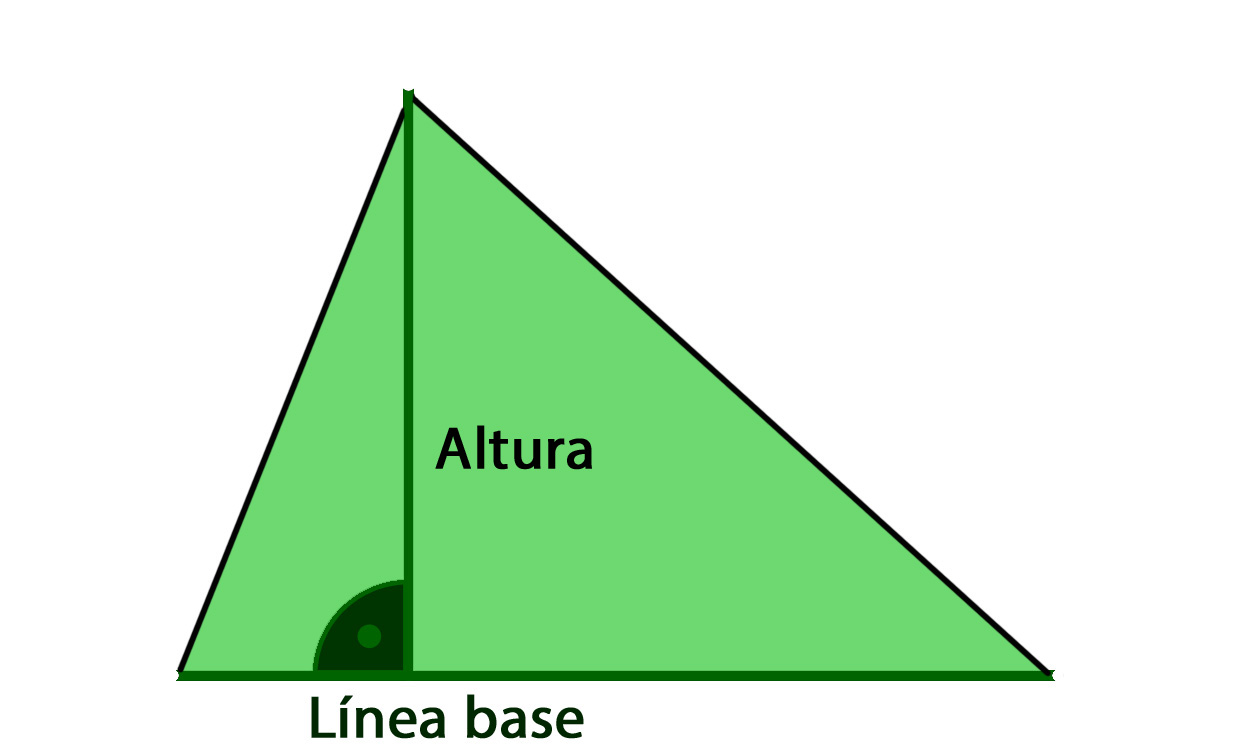
Área de un triángulo

Para calcular el área de un triángulo, existen varias posibilidades:

1- Cálculo con la línea de base y la altura asociada

• general

• Casos especiales para el triángulo rectángulo y para el triángulo equilátero

2- Cálculo con dos lados y el seno del ángulo entre ellos

3- Cálculo con un determinante (sólo posible en el sistema de coordenadas)

Calcular el área del triángulo con la línea de base y la altura

Este es el método más utilizado.

Para calcular el área triangular $A_{\mathrm{\Delta }}A\_\{\backslash Delta\}$ 

• la línea base $gg$ y

• la altura $hh$ del triángulo.

Diferentes versiones de la fórmula

La línea base $bb$ puede ser cualquier lado del triángulo; $hh$, sin embargo, debe ser la respectiva altura asociada.

Así, la fórmula puede aparecer de tres formas diferentes:

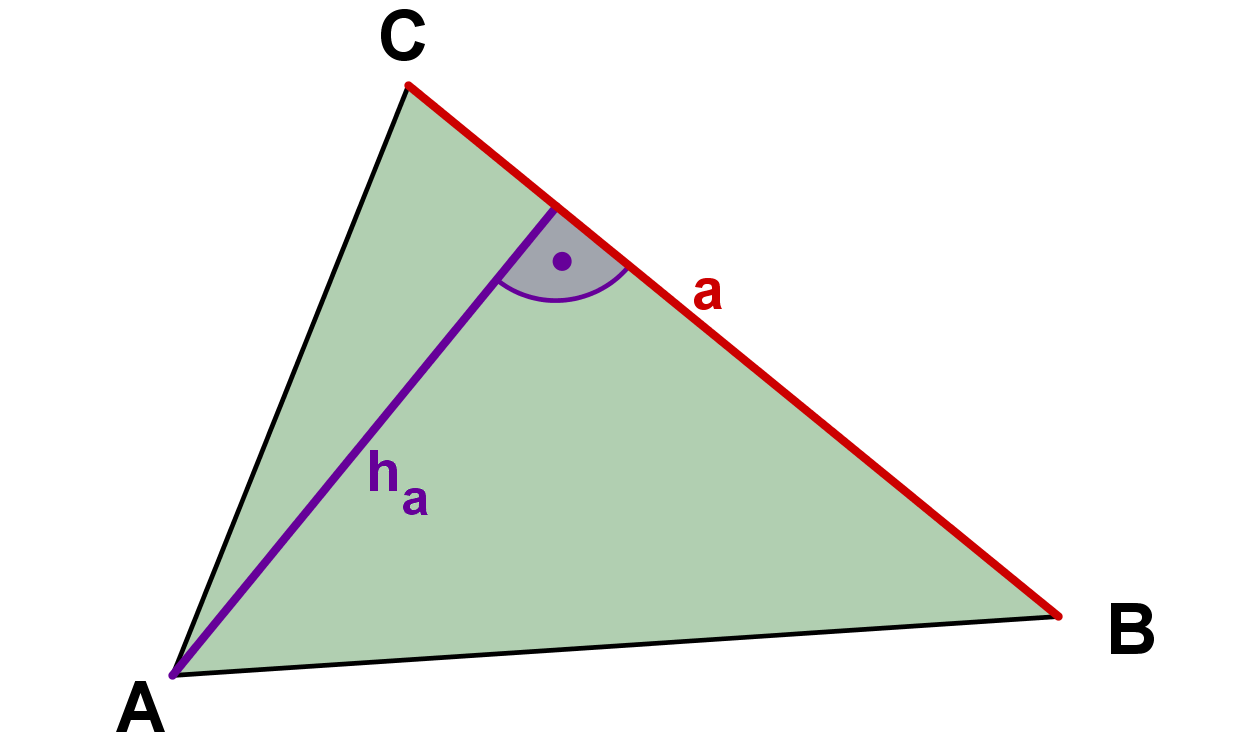
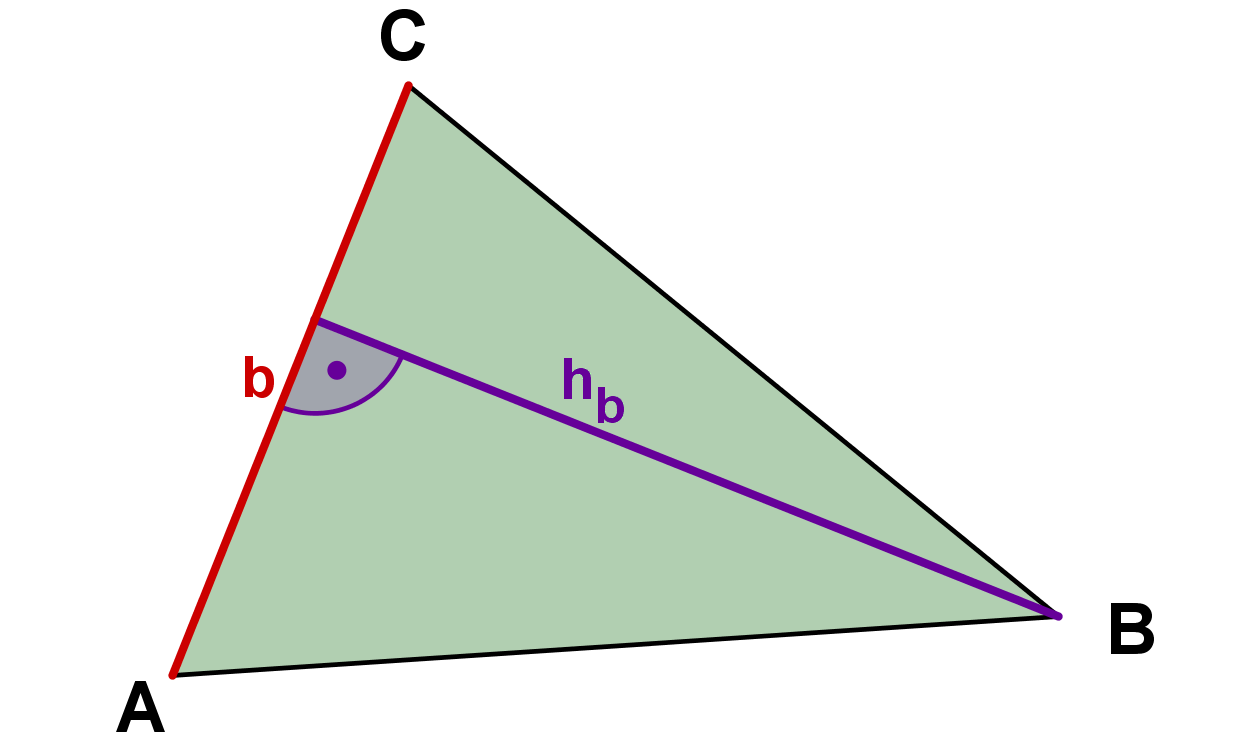
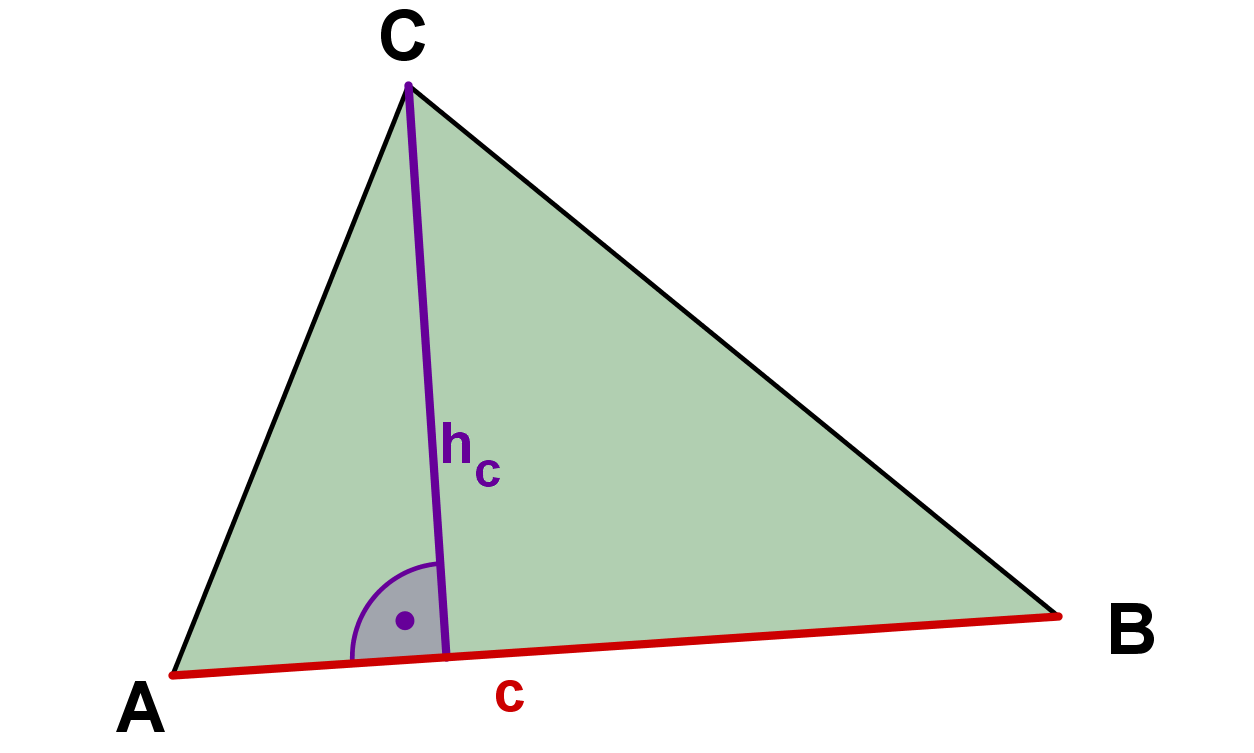
Caso especial: triángulo rectángulo

En un triángulo rectángulo con los lados $aa$ y $bb$ se aplica lo siguiente:

(La fórmula $A_{\mathrm{\Delta }ABC}=\frac{1}{2}\cdot c\cdot h_c\text{}A\_\{\backslash Delta\; ABC\}=\backslash frac\{1\}\{2\}\backslash cdot\; c\backslash cdot\; h\_c$ sigue siendo válida, por supuesto).

Caso especial: triángulo equilátero

En un triángulo equilátero de lado $aa$ se mantiene:

Calcular el área del triángulo con el seno

Si ya conoces y puedes utilizar el seno, también puedes calcular el área de un triángulo utilizando

• dos longitudes de lado y

• el seno del ángulo entre ellos

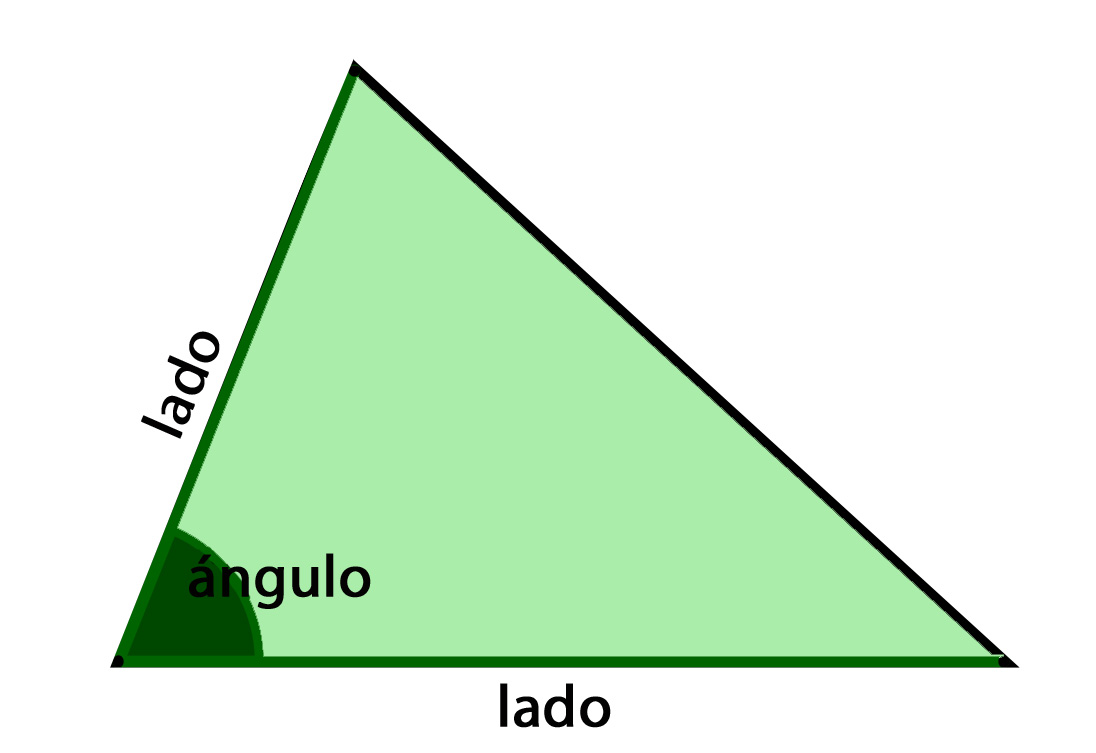
En lugar de $\gamma \backslash gamma$, por supuesto, se puede considerar cualquier otro ángulo del triángulo, y por lo tanto la fórmula puede aparecer de nuevo en tres formas diferentes:

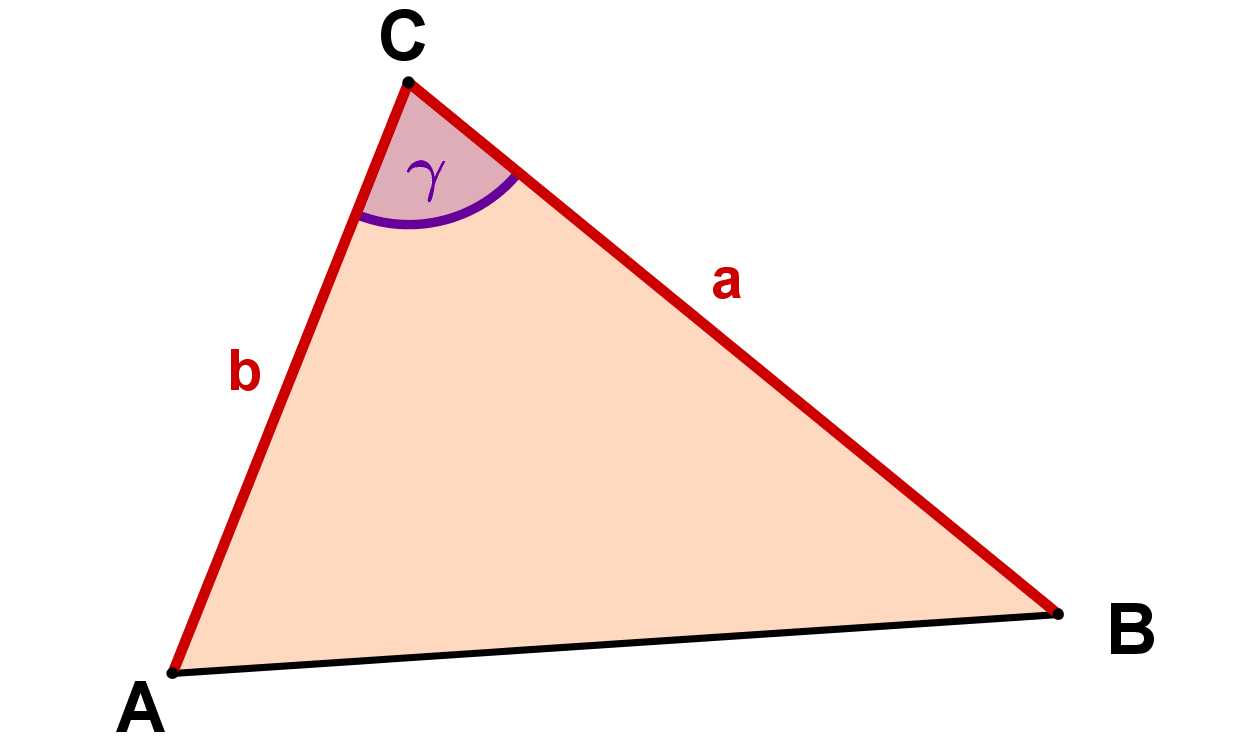
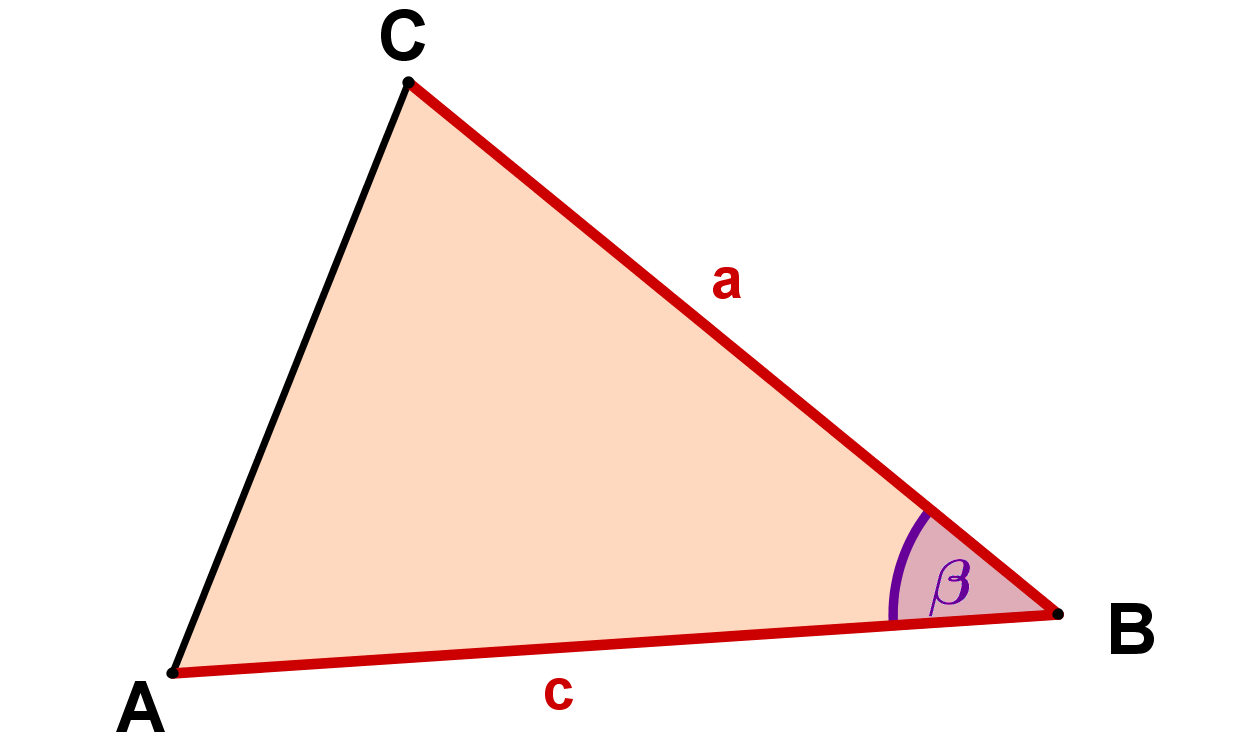
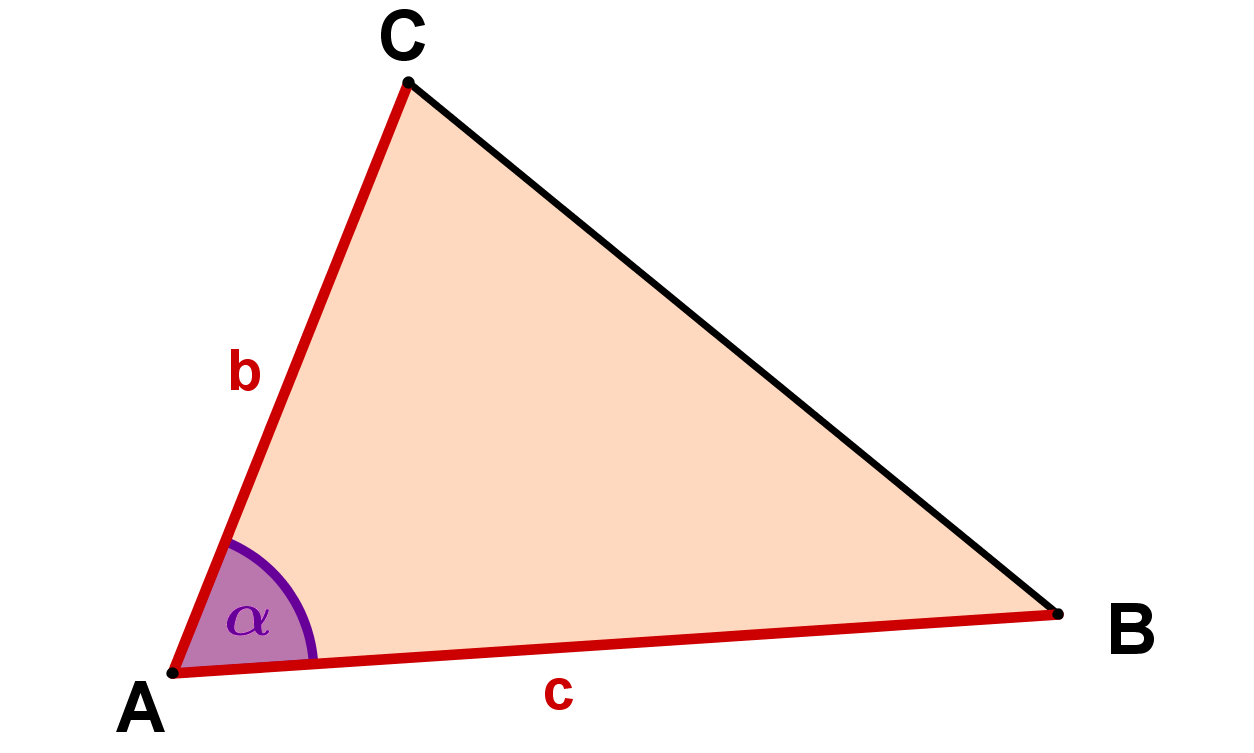
Calcular el área triangular con determinante

Por supuesto, este método sólo funciona si el triángulo está dado en un sistema de coordenadas.

haz clic aquí...