Calculando con fracciones
1 Suma y resta: fracciones con el mismo nombre
Tomás va a recibir su comida favorita hoy, ¡pizza! Corta la pizza en 12 trozos iguales. Una porción es la doceava parte de la pizza entera, es decir. .
Tomás se come trozos, es decir. , su amigo se come trozos, lo cual es .
¿Qué fracción de la pizza comen juntos?
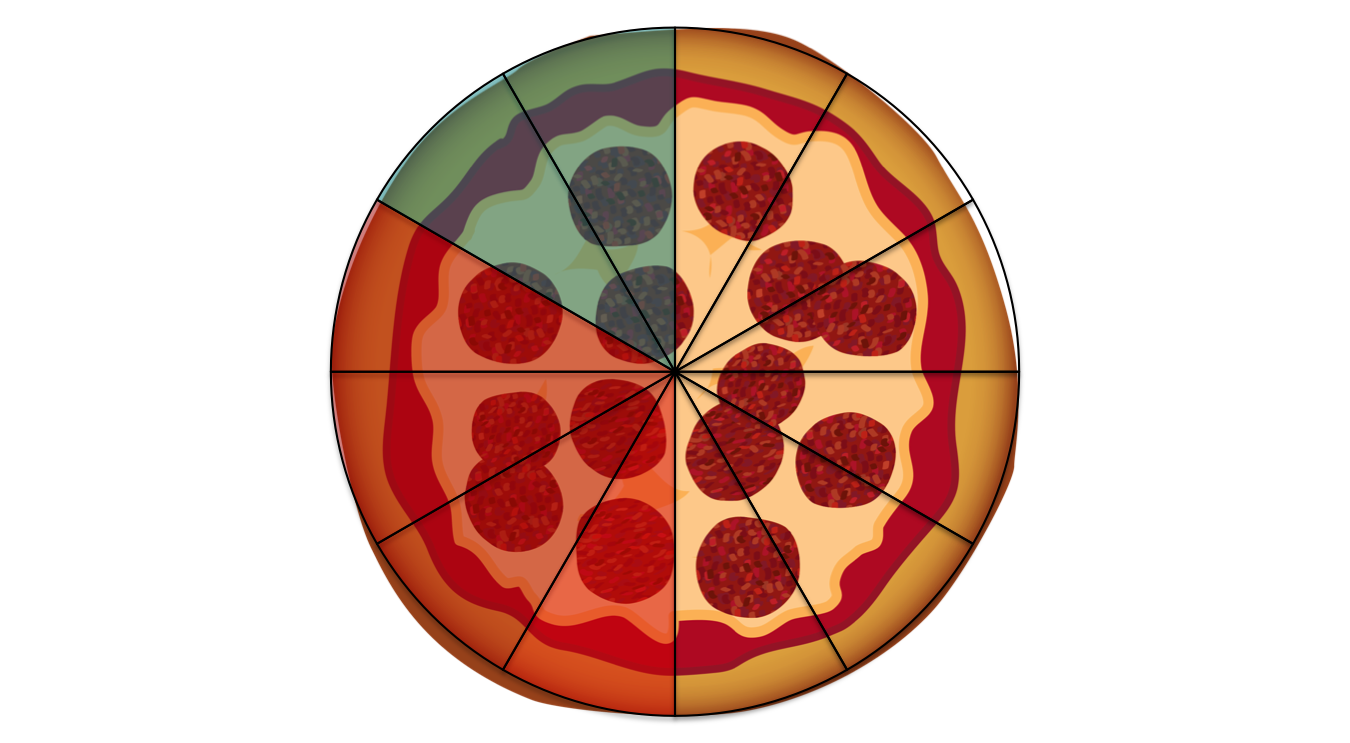
Los dos comieron juntos pedazos, y se representa con la fracción . Detrás está del cálculo está .
Así vemos que cuando se suman fracciones con el mismo nombre, los numeradores se suman mientras el denominador sigue siendo el mismo.
¿Qué fracción de la pizza sobra?
Como también se puede ver en el gráfico, quedan piezas, que es la fracción . Detrás de esto está el cálculo .
Nota:
Suma de fracciones con el mismo nombre: Los numeradores de las fracciones se suman, el denominador se mantiene: .
Resta de fracciones con el mismo nombre: Los numeradores de las fracciones se restan, el denominador se mantiene: .
A menudo, el resultado puede seguir reduciendo.
Ejercicios
Loading
2 Suma y resta: fracciones con nombre distinto
En el apartado anterior vimos cómo sumar y restar fracciones con el mismo nombre. Veamos ahora cómo calcular con fracciones que tienen diferentes denominadores, por ejemplo y .
Para ello, es útil ilustrar las fracciones mediante rectángulos:


Puedes ilustrar la suma colocando los dos rectángulos uno encima del otro.
Puedes ver que se forma una nueva división del rectángulo, en 6 partes. Hay partes de color turquesa y partes de color rojo. En total hay partes. Aquí hay que observar en la ilustración gráfica que las dos partes superiores de la izquierda deben contarse dos veces, ya que están coloreadas en ambos rectángulos.

Matemáticamente, lo que ocurre es lo siguiente La nueva descomposición corresponde a la ampliación del mismo denominador mayor:
Entonces puedes sumar estas dos fracciones como hemos visto antes, es decir, se suman los numeradores y el denominador sigue siendo el mismo:
Así, vemos que podemos calcular la suma de fracciones con nombres distintos expandiendo primero las fracciones al mismo denominador mayor. Podemos utilizar el mismo procedimiento para la resta.
Encuentra un denominador común.
Expande las fracciones hasta el común denominador
Suma o resta los numeradores
Reduce completamente el resultado
Ejercicios
Loading
3 Multiplicación: número natural por fracción
Volvamos a nuestro ejemplo de la pizza de antes: Tomás se comió trozos, es decir, la fracción , y su amigo se comió trozos, es decir . Así que su amigo se come el doble de piezas que Tomás. Detrás de esto está el cálculo

Ya sabes por los números naturales y enteros que: . Así que la multiplicación es una suma repetida.
Lo mismo ocurre al multiplicar números naturales por fracciones.
Así lo vemos:
Si multiplicamos un número natural por una fracción, el numerador se multiplica por ese número mientras el denominador sigue siendo el mismo.
Ejercicios
Loading
4 Multiplicación: fracción por número natural
Después de tanta pizza, Tomás y su amigo tienen sed. En el supermercado hay una botella de Cola de litros a la venta. Pero sólo consiguen beber de la botella.
¿Cuántos litros han bebido?

Debemos calcular los de los 2 litros. De forma gráfica, podemos pensarlo así:
Cada barra corresponde a 1 litro, de los cuales en cada caso se han bebido .
Así que se bebieron un total de . Así es:
de
Podemos calcularlo así:
de
Así que ya vemos:
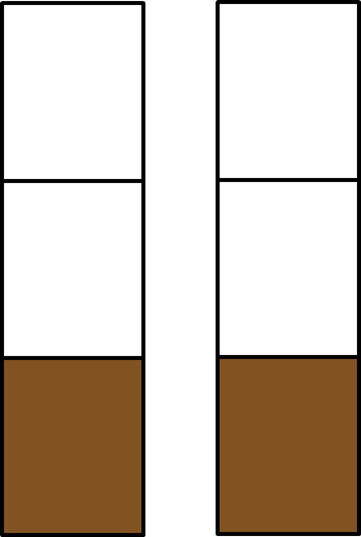
Si multiplicamos una fracción por un número natural, el numerador se multiplica por ese número mientras el denominador sigue siendo el mismo.
Ejercicios
Loading
5 Multiplicación: fracción por fracción
Tomás lleva consigo una caja de caramelos que todavía está llena. Tomás se come .
¿Qué cantidad del paquete original se comió Tomás ?

Por tanto, queremos saber qué tanto es de .
En primer lugar, visualizamos el dividiendo un rectángulo, que se supone que representa el paquete, en 4 partes iguales. También puedes volver a doblar lo mismo con una hoja de papel.

A continuación, ilustramos de la misma manera, dividiendo (doblando la hoja de papel) el rectángulo a lo largo en partes iguales.
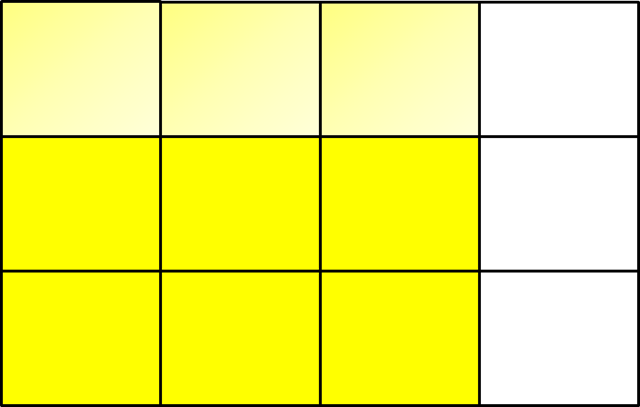
Ahora, si marcamos de , podemos contar que de la bolsa original están marcados.
Podemos calcularlo así:
de
Así que ya vemos:
Multiplicamos dos fracciones multiplicando el numerador por el numerador y el denominador por el denominador.
A menudo aún podemos reducir el resultado. En nuestro ejemplo podemos acortar el numerador y el denominador en y obtener:
Ejercicios
Loading
6 División: fracción dividida por un número entero
En el tema anterior hemos calculado que Tomás y su amigo han bebido juntos litros de cola. A la derecha se puede ver la cantidad de cola que se bebe.
Si ambos bebieron exactamente la misma cantidad, ¿cuántos litros de Coca bebió Tomás?
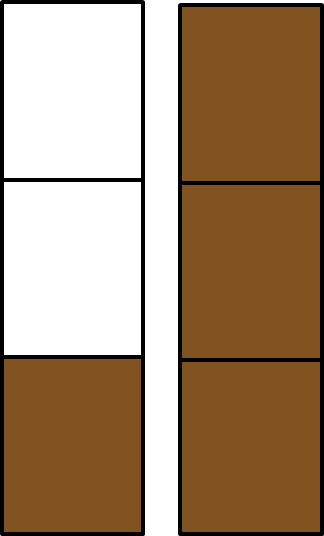
Así que tenemos que calcular dividido por . En términos generales, podemos pensar que cada una de las partes está dividida por la mitad.
Entonces podemos leer que Tomás bebió litros.
Así que es válido .
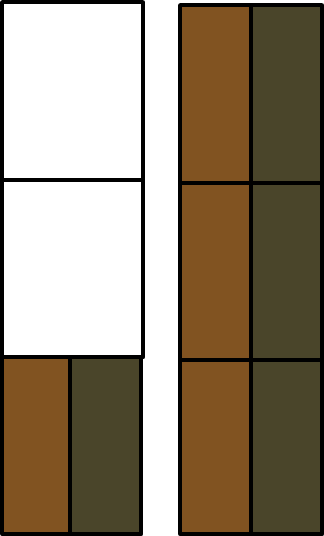
Otro ejemplo
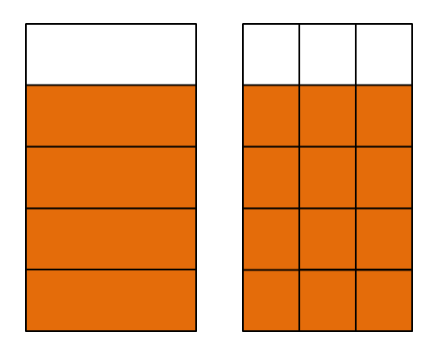
Ana, Lisa y María se reparten litros de jugo de manzana.
¿Cuánto jugo recibe Ana?

Dividimos cada una de las partes en partes iguales y podemos leerlas:
Así que Anna recibe litros de jugo de manzana.
Consideraciones sobre la regla de cálculo
Veamos con más detalle los cálculos de los dos ejemplos:
y
En el primer ejemplo, el significa que tomamos "la mitad" de . Así que también podemos escribir .
Asimismo, en el segundo ejemplo significa que tomamos la "tercera parte" de . Así que también podemos escribir .
Así, en lugar de dividir por un número entero, podemos multiplicar por la fracción invertida. Donde es la fracción invertida de y es la fracción invertida de 3.
Dividimos una fracción por un número entero multiplicando la fracción por la fracción invertida.
Ejercicios
Loading
Loading
7 División: fracción dividida por fracción
A Tomás y a su amigo les quedan litros de cola. Quieren decantarlas en botellas más pequeñas y manejables. Hay espacio para litros en cada botella pequeña.
¿Cuántas botellas necesitan?
Primero, veamos un ejemplo más sencillo. Si queremos llenar litros en botellas de 2 litros, calculamos: . Así que se necesitan 10 botellas para llenar litros en botellas de litros.
Del mismo modo, ahora podemos calcular cuántas botellas necesitan Tomás y su amigo. Calculamos:
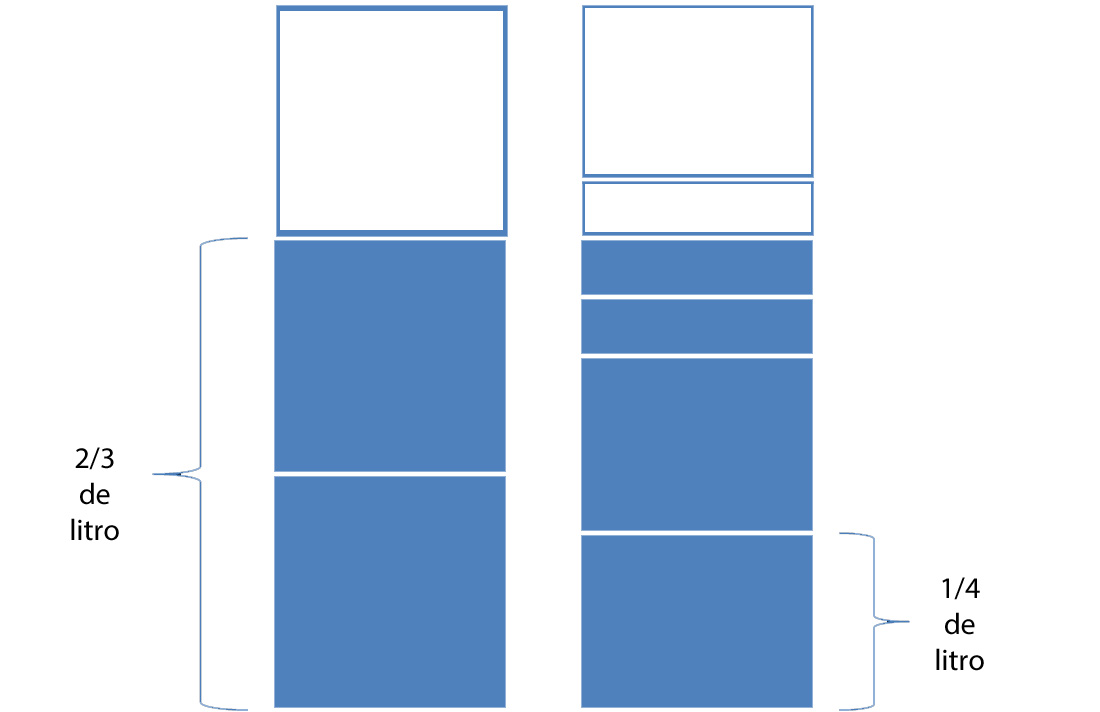
Intentemos visualizar de nuevo este cálculo. A la izquierda se ven los litros. A la derecha la misma cantidad de cola, pero en subdivisiones de litros. De esto podemos ver que Tomás y su amigo necesitan un total de botellas pequeñas. La tercera botella, sin embargo, sólo está llena hasta .
Entonces:
En el último paso, convertimos la fracción mixta.
En el capítulo anterior, aprendiste que en lugar de dividir por un número, podemos multiplicar por la fracción invertida. Lo mismo ocurre al dividir por una fracción.
Obtenemos fracción invertida de una fracción intercambiando el numerador y el denominador. Así, fracción invertida de es igual a y esta es .
Así que podemos calcular:
Nota:
Dividimos una fracción por otra multiplicando por la fracción invertida.