1 Descripción general
Contenido
En este curso aprenderás sobre las formas geométricas simples y sus propiedades.

Duración del curso
Se necesitan unos 30 minutos para este curso.
2 Formas geométricas básicas
3 Superficies redondas
Se pueden dividir muy bien las superficies según el número de sus esquinas.
0 Esquinas: superficies redondas
La circunferencia: es completamente redonda. Las luces de un semáforo, por ejemplo, tienen forma circular.

La elipse tiene más bien forma de un huevo. Es un círculo alargado en dos puntos. Algunas lonjas de pan, al cortarlas, tienen rebanadas con forma elíptica.

4 Triángulos
¿Por qué no hay ninguna superficie con una o dos esquinas?
No es posible dibujar una superficie con una sola "esquina". Aquí sólo tenemos un punto.
También con dos "esquinas" esto no funciona: Uno puede conectar estos sólo con una línea y así obtenemos un segmento.
3 esquinas: Triángulo
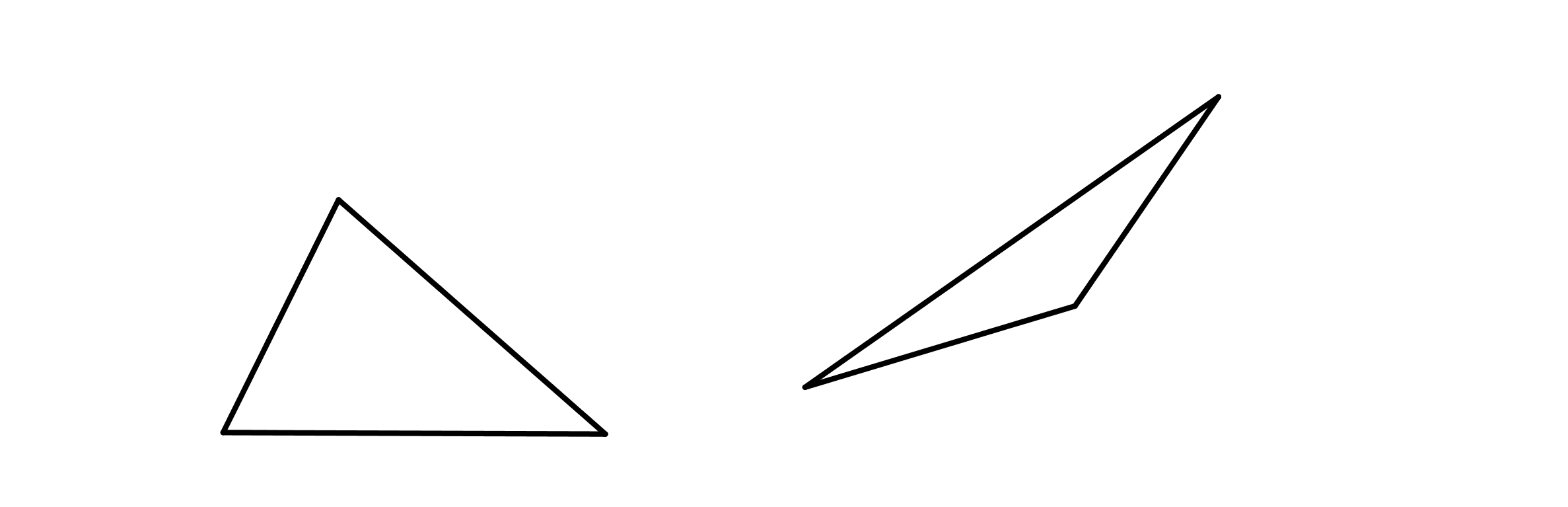
Un triángulo está formado por líneas y tiene -como su nombre indica- ángulos. En la escuela, por ejemplo, se utiliza una escuadra, y algunas señales de tránsito son triángulos.
5 Superficies con cuatro o más esquinas
4 ángulos: cuadrilatero
Conocemos algunos:
En un cuadrado, los cuatro lados tienen la misma longitud y los cuatro ángulos son de 90°. Por ejemplo, las caras de un cubo de juego son cuadrados.

En un rectángulo, los lados opuestos tienen la misma longitud y todos los ángulos son de 90°. Una hoja de papel es un ejemplo de rectángulo.
También en el paralelogramo los lados opuestos tienen la misma longitud. Sin embargo, aquí los ángulos no son todos iguales.

En el rombo, los cuatro lados tienen la misma longitud, pero los ángulos no son del mismo tamaño. Puedes encontrar rombos en naipes.
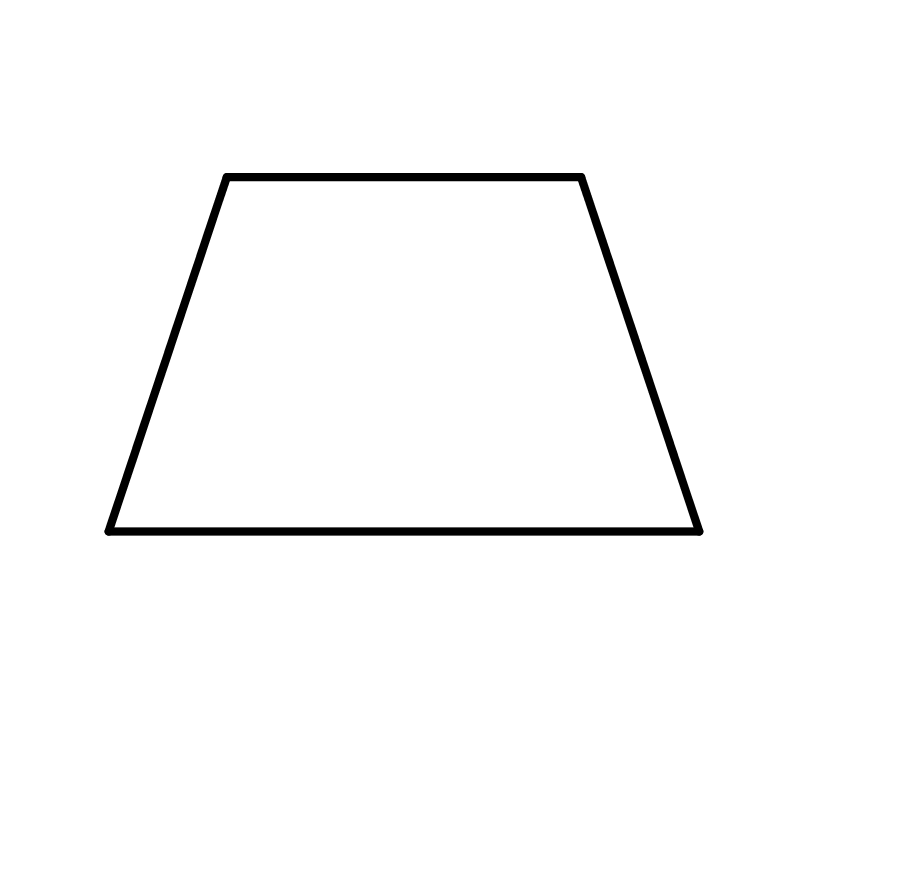
En el trapecio dos lados son paralelos entre sí, por lo que tienen la misma distancia entre sí
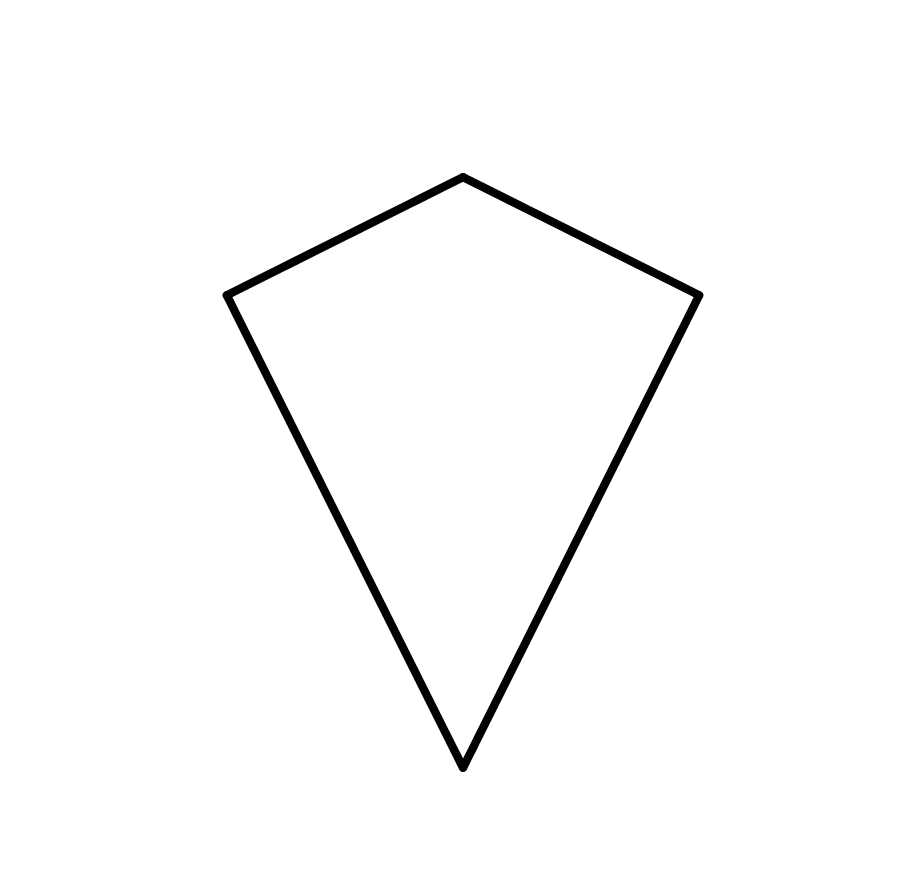
En el deltoide hay dos lados de igual longitud que se encuentran uno al lado del otro. El ejemplo es la cometa.
Observamos que las propiedades de algunos cuadriláteros son muy similares. Esto se debe a que algunos cuadriláteros están "relacionados" entre sí.
Más esquinas: polígonos
Podemos introducir tantas esquinas como queramos y la forma resultante sigue siendo una superficie.
Un ejemplo típico el hexágono con 8 esquinas como esta señal de pare.

6 Sólidos geométricos
Los cuerpos geométricos también se conocen como sólidos.
El cilindro
El cono
El cubo
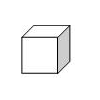
El hexaedro

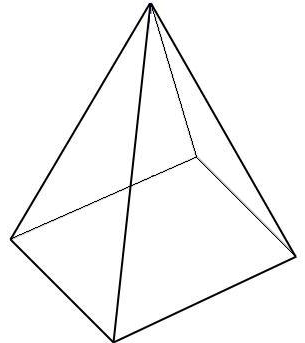
La pirámide
La esfera

7 Ejercicio sobre sólidos geométricos
Laden
Laden
8 Propiedades rectángulo y cuadrado
Dobla y corta una hoja de papel (tamaño carta o A4) como se muestra en la siguiente ilustración.

así obtienes dos nuevos cuadriláteros, concretamente un cuadrado y un rectángulo.
Si se comparan las longitudes de los lados de los respectivos cuadriláteros, se comprueba que:
Un cuadrado tiene cuatro lados de igual longitud.
En el rectángulo, los lados opuestos tienen la misma longitud.
Las propiedades del rectángulo y del cuadrado
Propiedades | rectángulo | cuadrado |
|---|---|---|
Los lados opuestos son paralelos. | x | x |
Los lados opuestos tienen la misma longitud. | x | x |
Todos los lados tienen la misma longitud. | x | |
Los lados colindantes son siempre perpendiculares entre sí. | x | x |
La figura tiene 4 ángulos rectos. | x | x |
Ejercicios:
Tarea 1: Dibuja rectángulos con las longitudes de los lados:
cm;cm
cm;cm
Tarea 2: Dibujar cuadrados con la longitud de los lados
cm
cm
cm
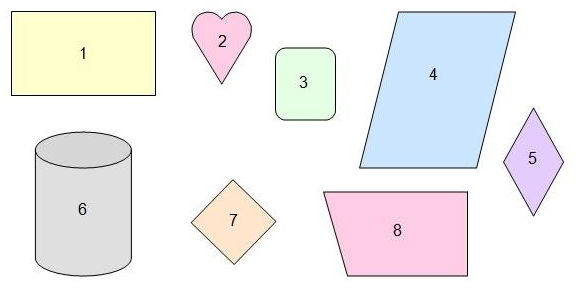
Tarea 3: ¿Cuáles de las siguientes figuras son rectángulos y cuáles son cuadrados? ¿Por qué?
9 Simetría
Coge una hoja de papel (tamaño carta o A4) y luego realiza los siguientes pasos:
Primero dobla la hoja por la mitad.
A continuación, dibuja una figura cualquiera a lo largo de la línea de plegado, como se muestra en el esquema de al lado.
Por último, recorta tu dibujo.
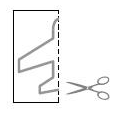
Una figura en la que las dos mitades coinciden exactamente al plegarse se tiene simetría axial.
La línea de plegado se llama eje de simetría.

Laden