Subconjunto de un conjunto

Definición

Un conjunto $A$ se denomina subconjunto del conjunto $B$ si cada elemento de $A$ es también un elemento de $B$ . Para esto escribe $A \subseteq B$ . Existe la posibilidad que $A = B$ .

Un subconjunto se denomina subconjunto propio si $A$ y $B$ no son las mismas cantidades, es decir, si $A \subseteq B$ y $A \neq B$ . Para esto la notación $A$ $⊊$ $B$ es usual.

Atención: La notación $A \subset B$ no se utiliza uniformemente en las matemáticas. $A$ veces significa que $A$ es un subconjunto de $B$ , a veces que es un subconjunto propio de $B$ .

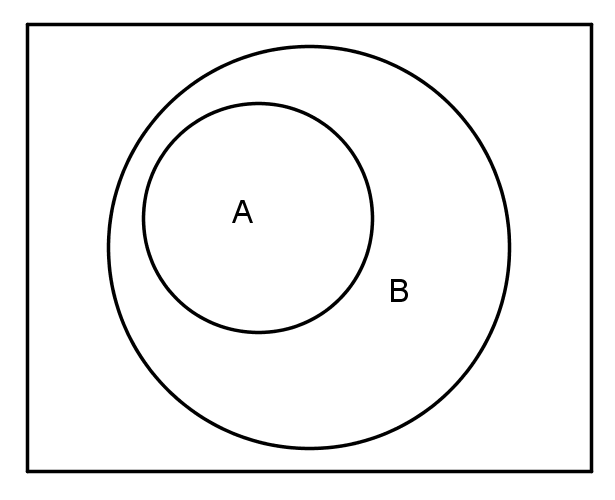
Ejemplo

Tenemos los conjuntos A y B respectivamente con

$A = {2; 3; a}$ y

$B = {1; 2; 3; a; b}$ .

Entonces $A \subseteq B$ , porque todos los elementos de $A$ están también contenidos en $B$ .

Observaciones

El conjunto vació se denota como $⌀$ .
$⌀ \subseteq A \subset G$ El conjunto vacío es un subconjunto de cada conjunto y cada conjunto debe ser un subconjunto del conjunto $G$ .
$A \subseteq A$ Cada conjunto es un subconjunto de sí mismo.
Si $A \subseteq B$ y $B \subseteq A$ , entonces $A$ y $B$ son la misma cantidad: $A = B$
Si $A \subseteq B$ y $B \subseteq C$ , entonceses también $A \subseteq C$ .
Cada conjunto es un subconjunto de la unión de sí mismo con otro conjunto $A \subseteq (A \cup B)$
El número cardinal de un subconjunto $A \subseteq B$ aplica: $| A | \leq | B |$

Conjunto Potencia

El conjunto Potencia $𝒫 (A)$ es el conjunto de todos los subconjuntos de $A$ .

Donde $A = (1,2,3)$ es $𝒫 (A) = (⌀, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3})$ .

Cabe señalar que este conjunto en sí mismo contiene conjuntos.

${1}$ y ${{1}}$ no son lo mismo.

El número cardinal $| 𝒫 (A) |$ , se puede calcular a través de $| 𝒫 (A) | = 2^{| A |}$ .

En cada subconjunto, cada elemento tiene 2 posibilidades, esté incluido o no.

Como ejemplo es entonces $| 𝒫 (A) | = 2^{| A |} = 2^{3} = 8$ .

Este contenido está licenciado bajo
CC BY-SA 4.0 → ¿Qué quiere decir esto? serlo.org