El teorema de Pitágoras establece una relación entre las longitudes laterales de un triángulo en ángulo recto:
La suma de los catéteres cuadrados (a y b) es igual al cuadrado de la hipotenusa (c).
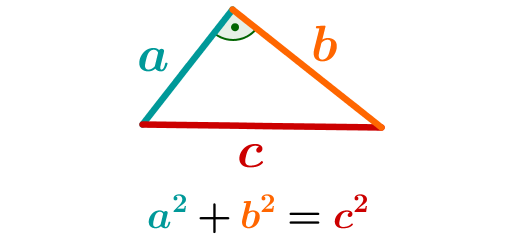
Ejemplo
Se dan los dos catetos a=4 y b=3 de un triángulo en ángulo recto.
Calcula la hipotenusa c.
Aplica el teorema de Pitágoras y calcula el lado derecho. | ||
saca la raíz | ||
(Nota: La solución está excluida, porque una longitud no puede ser negativa). |
Importante: Si está buscando un cateto tienes que usar esta fórmula:
Pitágoras también describe sperficies idénticas
Para cada número positivo , describe el área de un cuadrado con longitud lateral . De la misma manera, y pueden ser imaginados como el área de los cuadrados.
Así, el teorema de Pitágoras también da una relación de las áreas sobre el cateto y la hipotenusa en un triángulo en ángulo recto. Puedes ver esto claramente en el siguiente applet.
En un triángulo en ángulo recto, la suma de las áreas por encima de los catetos es igual al área del cuadrado por encima de la hipotenusa.
Aplicaciones
Los triángulos en ángulo recto son muy comunes. Por lo tanto, el teorema de Pitágoras tiene muchas aplicaciones.
Ejemplos de la práctica
Cálculo de las longitudes de ruta en las edificaciones
Cálculos sobre otras figuras y cuerpos
y así sucesivamente
Como una ayuda en el sistema de coordenadas
Para calcular la distancia entre dos puntos
Artefactos matemáticos
Espiral de Teodoro (para el dibujo exacto de las distancias de las longitudes , , )
