Para la creación de los contenidos de Serlo, utilizamos, especialmente en los campos de las matemáticas y la física, el programa de composición de fórmulas .
Esta página de ayuda tiene como obejetivo proporcionar apoyo técnico para el uso de .
Importante: En serlo.org el sólo se usa para escribir fórmulas, el texto normal no debe ser escrito en LaTeX.
Tabla de contenido
El entorno en el editor de Serlo
El entorno en el editor de Serlo
Antes de hablar de la correcta representación de las expresiones matemáticas, aquí verás primero cómo abrir el entorno de .
Paso 1:
Haz clic en el símbolo de la fórmula, que está marcado con unaflecha roja en la imagen.
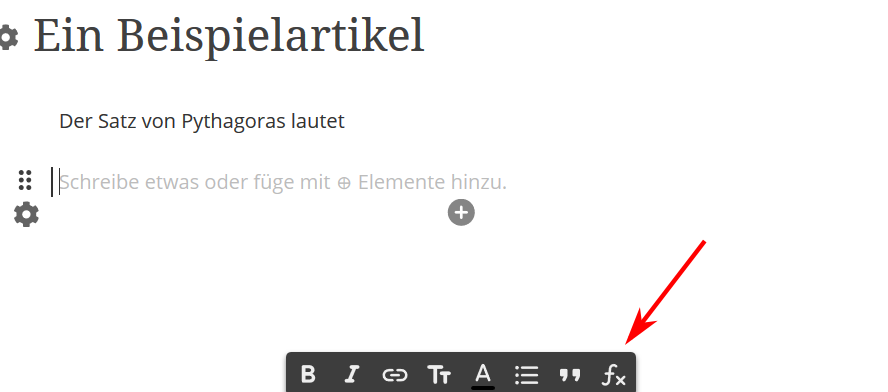
Paso 2:
Se abre la ventana que se muestra en la figura. Ahora selecciona la opción látex del menú desplegable.
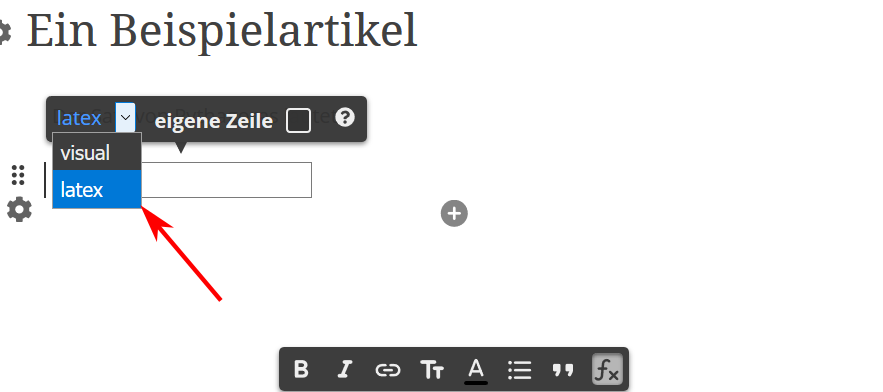
Todos los demás entornos, funciones y símbolos que se enumeran a continuación deben escribirse en este entorno para que se visualicen correctamente.
Notación matemática básica
Índices y exponentes
Los índices se crean dentro del entorno usando el comando _. Para los exponentes se utiliza ^. Si el índice o exponente contiene más de un carácter, los dos comandos mencionados anteriormente deben ser extendidos por { }. De la siguiente manera _{ } y ^{ } respectivamente.
Edición | Codigo LaTeX | Explicación |
|---|---|---|
x^2 | Exponentes con circunflejo: ^ | |
x^{2a} | Los exponentes con dos o más caracteres entre corchetes | |
x_1 | Índices con guión bajo: _ | |
x_{1,2} | Índices con dos o más caracteres entre corchetes |
Funciones trigonométricas
Para la correcta notación de las funciones trigonométricas, observe que en lugar de usar simplemente sin(x), usa el comando \sin(x).
Esta regla también se aplica a todas las demás funciones trigonométricas. Aquí se puede desplegar una tabla donde se encuentran los comandos correspondientes.
Expresiones de raíz
La representación con símbolos que utilizan radical es posible dentro del ambiente con el
comando \sqrt{ }. Este comando representa la raíz cuadrada por defecto.
Si necesitas la n-ésima raíz en general, usa el comando \sqrt[ ]{}.
Edición | Codigo LaTeX | Explicación |
|---|---|---|
\surd | Símbolo de raíz sin radical | |
\sqrt{x} | Raíz cuadrada | |
\sqrt[a]{x} | Raices más altas |
Fracciones
Para las fracciones se utiliza el comando \dfrac{ }{ }. El contenido dentro de la primera llave { } representa el numerador de la fracción, mientras que el contenido dentro de la segunda llave { } representa el denominador de la fracción.
Edición | Codigo LaTeX | Explicación |
|---|---|---|
\dfrac{3+x}{2x} | Para las fracciones, el numerador y el denominador entre llaves. |
El alfabeto griego
El texto en el entorno
Ocasionalmente sucede que dentro de un entorno se requiere texto además de fórmulas y ecuaciones. Para hacerlo, usa el comando \text{ }. Este comando es especialmente importante en la física, ya que se utiliza para mostrar las unidades correctamente.
Ejemplo:
Codigo LaTeX de entrada | resultado |
|---|---|
a = 3 \ \dfrac{\text{m}}{\text{s}^2} |
Colores
También puede dar color a secciones de su fórmula, por ejemplo para marcar un paso importante en un cálculo. Esto funciona con el comando \textcolor{}{}.
En la primera llave, introduce el código hexadecimal del color que desea utilizar.
Ejemplo:
Se escribe asi en LaTex:
\textcolor{009999}{\text{este texto tiene el color con el código hexadecimal 009999}}
.
Se escribe asi en LaTex:
\textcolor{cc0000}{\text{este texto tiene el color con el código hexadecimal cc0000}}
Los códigos hexadecimales de los colores recomendados en Serlo se encuentran en la página de ayuda para imágenes y gráficos.
En la segunda llave se introduce el código que sequiere resaltar en color.
Codigo de entrada:
f(x) = \textcolor{ff6600}{1013}\cdot \textcolor{009999}{1,42}^x = \textcolor{ff6600}{a}\cdot \textcolor{009999}{b}^x
Resultado:
Paréntesis y soportes
Los paréntesis se escriben siempre con \left y \right, para que se adapten al tamaño de la fórmula en el medio.A continuación tienes una lista de la notación de paréntesis más importante.
Para el valor abosoluto también puedes poner líneas de cantidad con \left y \right.
Codigo de entrada:
f(x)=\left| x \right|
Resultado:
Vectores, matrices y determinantes
Para vectores y matrices se necesita un entorno adicional dentro del entorno :
Vectores y matrices
Entorno | Uso | |
|---|---|---|
pmatrix | Con el entorno "pmatrix" se pueden crear vectores y matrices. Las líneas se terminan con \\. Las columnas individuales de una matriz se separan con &. |
Codigo pmatrix de entrada:
\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}
Resultado:
Codigo pmatrix de entrada:
A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}
Resultado:
Determinantes
El siguiente entorno se utiliza para representar los determinantes:
Entorno | Uso | |
|---|---|---|
vmatrix | El entorno "vmatrix" es útil para la notación de los determinantes. Las líneas se terminan con \\. Las columnas individuales de una matriz se separan con &. |
Codigo vmatrix de entrada:
\det A = \begin{vmatrix} 2 & 2 & 5 \\ 1 & 3 & 9 \\ 2 & 3 & 4 \end{vmatrix}
Resultado:
Integrales
Para mostrar las integrales, se utiliza el comando \int. Sino es indefinida, los límites inferior y superior pueden ser complementados adicionando \int_{ }^{ }. El contenido del par de paréntesis después del comando _ determina el límite inferior, mientras que el contenido del par de paréntesis después del comando ^ determina el contenido del límite superior.
Edición | Codigo LaTeX | Explicación |
|---|---|---|
\int_{-\pi}^{\pi} \sin(x) \mathrm{d}x | Límites integrales con _ y ^, y el operador "d" en notación normal con \mathrm{}. |
Al mostrar las variables de integración, ten en cuenta de no escribir dx, sino de usar el comando \mathrm{d}x en su lugar.
Flechas
Lista de expresiones matemáticas
Funciones
Símbolos especiales
Escritura y otros caracteres especiales
Aquí puedes encontrar caracteres especiales, las flechas de vectores, y otros:
