Vector

Un vector denota un desplazamiento y se representa por cualquier flecha

que sea la misma longitud y
la misma dirección

como el desplazamiento en cuestión.

Los vectores se suelen nombrar con una letra minúscula con una flecha encima. Así, los nombres típicos de los vectores son $\vec{a}, \vec{v}, \vec{w} \dots$

Las flechas individuales se llamans de este vector. Todos son paralelos entre sí.

Aquí puedes ver algunas equivalentes del vector $\vec{a}$ .

Al hacer clic en la imagen o en el botón superior, aceptas que se cargará el contenido externo de GeoGebra . También los datos personales pueden ser transferidos a este servicio de acuerdo con nuestro Política de privacidad.

Introducción detallada

Vídeo de introducción al concepto de vectores

Investiga en la gráfica

En el applet puedes seleccionar los puntos A y B y la flecha vectorial $\vec{v}$ . Investiga cuando el vector cambia.

Vectores en el plano y en el espacio

El vector $\vec{a} = (\begin{array}{c} 2 \\ 3 \end{array})$ se encuentra en el plano x-y

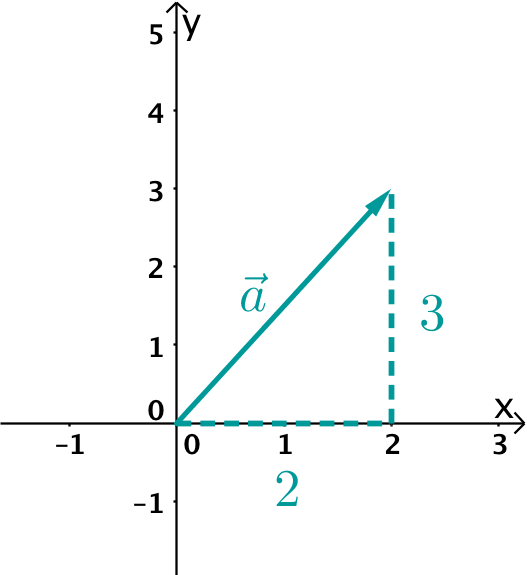
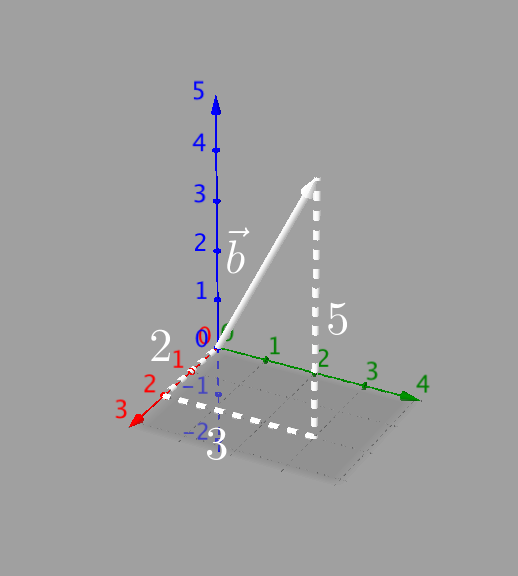
El vector $\vec{b} = (\begin{array}{c} 2 \\ 3 \\ 5 \end{array})$ se encuentra en el espacio.

Las coordenadas de un vector $\vec{v}$ se designan con diferentes notaciones. Algunos ejemplos son:

\vec{v} = (\begin{array}{c} x_{v} \\ y_{v} \end{array})

\vec{v} = (\begin{array}{c} v_{1} \\ v_{2} \end{array})

\vec{v} = (\begin{array}{c} v_{x} \\ v_{y} \end{array})

Longitud de un vector

La longitud o magnitud de un vector $\vec{a}$ se denota por $| \vec{a} |$ (o a menudo $‖ \vec{a} ‖$ ) y se calcula como sigue:

$‖ \vec{a} ‖ = \sqrt{a_{1}^{2} + a_{2}^{2}}$ , si $\vec{a}$ se encuentra en el plano.

$‖ \vec{a} ‖ = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}$ , si $\vec{a}$ se encuentra en el espacio.

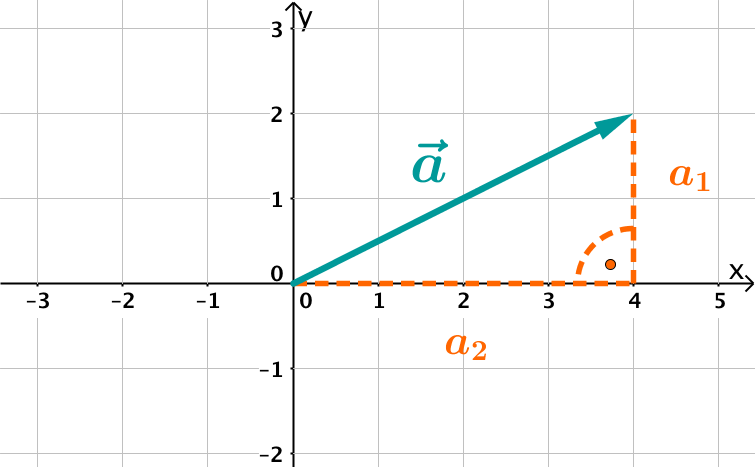
Relación entre dos vectores

Paralelismo

Dos vectores $\vec{v}$ y $\vec{w}$ son paralelos entre sí si uno es múltiplo del otro:

$\vec{v} = k \cdot \vec{w} k \in ℝ$

Ortogonalidad

Dos vectores $\vec{a}$ y $\vec{b}$ son ortogonales (= perpendiculares) entre sí si su producto escalar es a ∘ b es igual a $0$ .

Un vector $\vec{n}$ que es ortogonal

a otro vector $\vec{v}$ o
a una recta $g$ o
a un plano $E$

se llama vector normal de $\vec{v}$ , $g$ o $E$ .

Especialmente los planos, pero también las rectas, se representan de forma muy sencilla con vectores normales en una forma normal.

Cálculos con vectores

Los vectores pueden calcularse de forma similar a los números. Por lo tanto, puedes:

Suma y resta de vectores,
con un número escalar multiplicar vectores (= estirar o comprimir),
multiplica dos vectores entre sí.

Importante: Hay más de una forma de multiplicar vectores entre sí. Con el producto escalar el resultado es un número (= un escalar), mientras que con el producto cruzado sale otro vector.

Otro cálculo importante que puede hacerse con vectores es la llamada multiplicación matriz-vector.

Still want more?

You can find more content on this topic here:

Articles

Este contenido está licenciado bajo
CC BY-SA 4.0 → ¿Qué quiere decir esto? serlo.org